
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

【答案】(1)见解析;(2)四边形ABCD的面积=6![]() cm2.
cm2.
【解析】
(1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
(2)解直角三角形求得菱形的边长,根据平行四边形的面积公式求得即可.
(1)过点A作AE⊥BC于E,AF⊥CD于F,

∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵SABCD=BCAE=CDAF.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形;
(2)在Rt△AEB中,∠AEB=90°,∠ABC=60°,AE=3cm,
∴AB=![]() =2
=2![]() cm,
cm,
∴BC=2![]() cm,
cm,
∴四边形ABCD的面积=AEBC=6![]() cm2.
cm2.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球![]() 每个球除颜色外都相同
每个球除颜色外都相同![]() 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验![]() 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
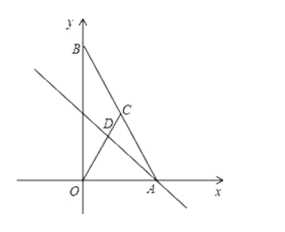
【题目】如图,在平面直角坐标系中,![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上,
上,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() 上一动点(不与
上一动点(不与![]() 重合),
重合),![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:① x2+y2=49;② x﹣y=2;③ x+y=9;④ 2xy+4=49;其中说法正确的是( )

A. ①②B. ①②④
C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
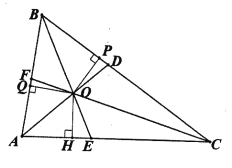
【题目】已知在△ABC中,∠BAC=![]() ,∠ABC=
,∠ABC=![]() ,∠BCA=
,∠BCA=![]() ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
(1)若![]() =78°,
=78°,![]() =56°,
=56°,![]() =46°,求∠EOH的大小;
=46°,求∠EOH的大小;
(2)用![]() ,
,![]() ,
,![]() 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
(3)若![]() ≥
≥![]() ≥
≥![]() ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ=![]() ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com