
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 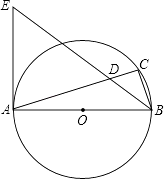
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
【答案】
(1)90°;直径所对的圆周角是直角
(2)解:△EAD是等腰三角形.
证明:∵∠ABC的平分线与AC相交于点D,
∴∠CBD=∠ABE
∵AE是⊙O的切线,∴∠EAB=90°
∴∠AEB+∠EBA=90°,
∵∠EDA=∠CDB,∠CDB+∠CBD=90°,
∵∠CBE=∠ABE,
∴∠AED=∠EDA,
∴AE=AD
∴△EAD是等腰三角形
(3)解:解:∵AE=AD,AD=6,
∴AE=AD=6,
∵AB=8,
∴在直角三角形AEB中,EB=10
∵∠CDB=∠E,∠CBD=∠ABE
∴△CDB∽△AEB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
∴设CB=4x,CD=3x则BD=5x,
∴CA=CD+DA=3x+6,
在直角三角形ACB中,
AC2+BC2=AB2
即:(3x+6)2+(4x)2=82,
解得:x=﹣2(舍去)或x= ![]()
∴BD=5x= ![]()
【解析】解:(1)∵AB是⊙O的直径,点C在⊙O上,∴∠ACB=90°(直径所对的圆周角是直角) (1)根据AB是⊙O的直径,点C在⊙O上利用直径所对的圆周角是直角即可得到结论;(2)根据∠ABC的平分线与AC相交于点D,得到∠CBD=∠ABE,再根据AE是⊙O的切线得到∠EAB=90°,从而得到∠CDB+∠CBD=90°,等量代换得到∠AED=∠EDA,从而判定△EAD是等腰三角形.(3)证得△CDB∽△AEB后设BD=5x,则CB=4x,CD=3x,从而得到CA=CD+DA=3x+6,然后在直角三角形ACB中,利用AC2+BC2=AB2得到(3x+6)2+(4x)2=82解得x后即可求得BD的长.


科目:初中数学 来源: 题型:
【题目】在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 ![]() 千米的C处.
千米的C处.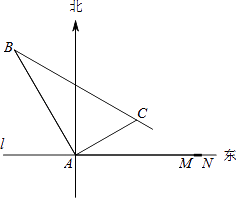
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=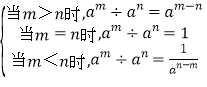
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:![]() = ,43÷45= .
= ,43÷45= .
(2)如果 3x-1÷33x-4=![]() ,求出 x 的值.
,求出 x 的值.
(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为 . (精确到1m)
【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】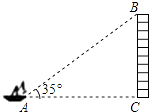
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)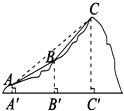
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() .(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)
.(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)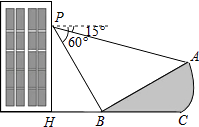
(1)∠PBA的度数等于度;(直接填空)
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com