
分析 根据题意画出图形,∴△OAM是等边三角形,易知M($\sqrt{3}$,1)或(-$\sqrt{3}$,1,利用待定系数法即可解决问题.
解答 解:如图,∵AM=OM=OA=2,
∴△OAM是等边三角形,
易知M($\sqrt{3}$,1)或(-$\sqrt{3}$,1)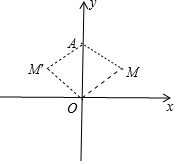
当M($\sqrt{3}$,1)时,1=2$\sqrt{3}$+b,解得b=1-2$\sqrt{3}$,
当M(-$\sqrt{3}$,1)时,1=-2$\sqrt{3}$+b,解得b=1+2$\sqrt{3}$,
故答案为:1-2$\sqrt{3}$或1+2$\sqrt{3}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
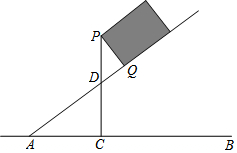 一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.
一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它与3πa2b是同类项 | B. | 它的系数是3 | ||
| C. | 它是二次单项式 | D. | 它与$-\frac{7}{2}{a^2}b$的和是2a2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
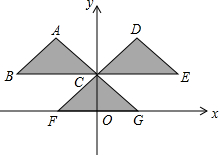 如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).
如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com