
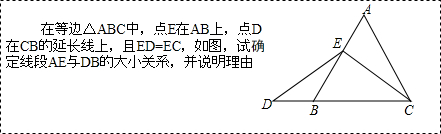
分析 (1)根据等边三角形性质和等腰三角形的性质求出∠EDB=∠BCE=30°,求出∠DEB=30°,求出BD=BE即可;
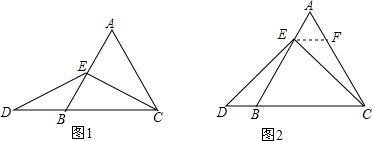
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由三角形相似利用比例关系求出CD=6,当E在BA的延长线上,D在BC的延长线上时,求出CD=2.
解答 解:
(1)∵△ABC是等边三角形,E为AB的中点,
∴∠BCE=30°,BE=AE,
∵ED=EC,
∴∠EDB=∠BCE=30°,
∵∠ABD=120°,
∴∠DEB=30°,
∴DB=EB,
∴AE=DB,
故答案为:=;
(2)AE=DB.
如图2,过点E作EF∥BC,交AC于点F.
∵EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°.
∴△AEF是等边三角形,AE=EF=AF.
∴BE=CF.
∵ED=EC,
∴∠ECD=∠D.
又∵∠ECF=60°-∠ECD,∠DEB=∠EBC-∠D=60°-∠D,
∴∠ECF=∠DEB.
在△BDE与△FEC中,
$\left\{\begin{array}{l}{BE=CF}\\{∠ECF=∠DEB}\\{ED=EC}\end{array}\right.$
∴△BDE≌△FEC(SAS),
∴BD=EF=AE.
∴AE=DB.
故答案为:=;
(3)解:CD=6或2,
分为两种情况:
①如图3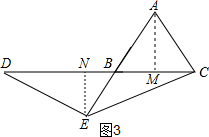
过A作AM⊥BC于M,过E作EN⊥BC于N,
则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∵AM⊥BC,
∴BM=CM=$\frac{1}{2}$BC=1,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴$\frac{AB}{BE}$=$\frac{BM}{BN}$,
∴$\frac{2}{4-2}$=$\frac{1}{BN}$,
∴BN=1,
CN=2+1=3,
∴CD=2CN=6;
②如图4,作AM⊥BC于M,过E作EN⊥BC于N,则AM∥EN,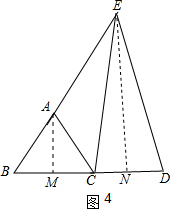
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∵AM⊥BC,
∴BM=CM=$\frac{1}{2}$BC=1,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴$\frac{AB}{AE}$=$\frac{BM}{BN}$,
∴$\frac{2}{4}$=$\frac{1}{MN}$,
∴MN=2,
∴CN=2-1=1,
∴CD=2CN=2,
综上所述CD=6或2,
故答案为:2或6.
点评 本题为三角形的综合应用,涉及等边三角形的性质、全等三角形的判定和性质、等腰三角形的性质、三角形外角的性质、相似三角形的判定和性质及分类讨论思想等知识点.第(3)题是难点,解题的关键是确定出有2种情况,求出每种情况的CD值.本题考查知识点较多,综合性较强,难度适中.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
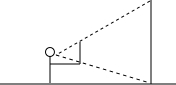 如图,一个人拿着一把厘米刻度尺,站山在距电线杆30m的地方,把甲臂向前伸直,刻度尺竖直,尺上0-12cm这一段恰好遮住电线杆.若手臂的长为60cm.求电线杆的高度.
如图,一个人拿着一把厘米刻度尺,站山在距电线杆30m的地方,把甲臂向前伸直,刻度尺竖直,尺上0-12cm这一段恰好遮住电线杆.若手臂的长为60cm.求电线杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com