
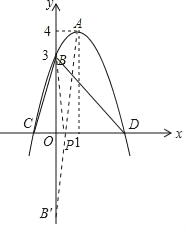
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=﹣(x﹣1)2+4;(2)当PA+PB的值最小时的点P的坐标为(![]() ,0);(3)点Q的坐标为(2,3)或(1﹣
,0);(3)点Q的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).
【解析】
(1)设抛物线顶点式解析式y=a(x-1)2+4,然后把点B的坐标代入求出a的值,即可得解;(2)先求出点B关于x轴的对称点B′的坐标,连接AB′与x轴相交,根据轴对称确定最短路线问题,交点即为所求的点P,然后利用待定系数法求一次函数解析式求出直线AB′的解析式,再求出与x轴的交点即可.(3)S△CDQ=S△BCD且CD是两三角形的公共底边知|yQ|=yB=3,据此得yQ=3或yQ=-3,再分别求解可得.
解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)点B关于x轴的对称点B′的坐标为(0,﹣3),
由轴对称确定最短路线问题,连接AB′与x轴的交点即为点P,
设直线AB′的解析式为y=kx+b(k≠0),
则![]() ,
,
解得![]() ,
,
∴直线AB′的解析式为y=7x﹣3,
令y=0,则7x﹣3=0,
解得x=![]() ,
,
所以,当PA+PB的值最小时的点P的坐标为(![]() ,0).
,0).
(3)∵S△CDQ=S△BCD,且CD是两三角形的公共底边,
∴|yQ|=yB=3,
则yQ=3或yQ=﹣3,
当yQ=3时,﹣(x﹣1)2+4=3,
解得:x=0或x=2,
则点Q(2,3);
当yQ=﹣3时,﹣(x﹣1)2+4=﹣3,
解得:x=1﹣![]() 或x=1+
或x=1+![]() ,
,
则点Q坐标为(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3);
,﹣3);
综上,点Q的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).


科目:初中数学 来源: 题型:
【题目】某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4:17:15。

根据这四名同学提供的材料,下面有四个推断:
①这次跳绳测试共抽取了150人;②该年级跳绳次数的中位数在115~125之间
③第4组的人数为45人 ④如果跳绳次数不少于135次为优秀,根据这次调查结果,估计全年级达到跳绳优秀的人数可以超过250人,其中合理的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.

(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
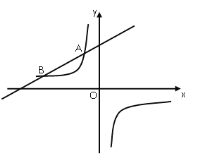
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、![]() 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在![]() 中,两边长分别为
中,两边长分别为![]() ,且且
,且且![]() ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:Rt![]() 中,
中,![]() ,且b>a,若Rt
,且b>a,若Rt![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=﹣![]() 的图象上,点D在反比例函数y=
的图象上,点D在反比例函数y=![]() (k≠0)的图象上,AD∥x轴,AB⊥x轴于B,DC⊥x轴于C,若OB=
(k≠0)的图象上,AD∥x轴,AB⊥x轴于B,DC⊥x轴于C,若OB=![]() OC,则k的值为_____.
OC,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() 的度数是 ;
的度数是 ;
(2)若![]() ,
,![]() 的周长是
的周长是![]() .
.
①求![]() 的长度;
的长度;
②若点![]() 为直线
为直线![]() 上一点,请你直接写出
上一点,请你直接写出![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com