
【题目】成都至西安的高速铁路(简称西成高铁)全线正式运营,至此,从成都至西安有两条铁路线可选择:一条是普通列车行驶线路(宝成线),全长825千米;另一条是高速列车行驶线路(西成高铁),全长660千米,高速列车在西成高铁线上行驶的平均速度是普通列车在宝成线上行驶的平均速度的3倍,乘坐普通列车从成都至西安比乘坐高速列车从成都至西安多用11小时,则高速列车在西成高铁上行驶的平均速度是多少?
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他离家的距离与时间的变化情况如图所示.

(1)10时时他离家 ![]() ,他到达离家最远的地方时是 时,此时离家
,他到达离家最远的地方时是 时,此时离家 ![]() ;
;
(2)他可能在哪段时间内休息,并吃午餐?
(3)他在出行途中,哪段时间内骑车速度最快,速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家春天粉刷房间,雇用了5个工人,做了10天完工。用了某种涂料150升,费用为4800元;粉刷的面积为150![]() 。最后结算工钱时有以下几种方案:
。最后结算工钱时有以下几种方案:
方案1:按工算,每个工30元;(1个工人做一天是一个工)
方案2:按涂料费用算,涂料费用的30%作为工钱;
方案3:按粉刷面积算,每平方米付工钱12元。
请你帮小红家出主意,选择那种方案付钱最合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
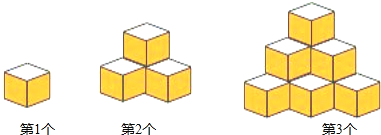
【题目】现用棱长为2cm的小立方体按如图所示规律搭建几何体,图中自上面下分别叫第一层、第二层、第三层…,其中第一层摆放1个小立方体,第二层摆放3个小立方体,第三层摆放6个小立方体…,那么搭建第1个小立方体,搭建第2个几何体需要4个小立方体,搭建第3个几何体需要10个小立方体…,按此规律继续摆放.
(1)搭建第4个几何体需要小立方体的个数为 ;
(2)为了美观,需将几何体的所有露出部分(不包含底面)都喷涂油漆,且喷涂1cm2需用油漆0.2克.
①求喷涂第4个几何体需要油漆多少克?
②如果要求从第1个几何体开始,依此对第1个几何体,第2个几何体,第3和几何体,…,第n个几何体(其中n为正整数)进行喷涂油漆,那么当喷涂完第21个几何体时,共用掉油漆多少克?
(参考公式:①1×2+2×3+3×4+…+n(n+1)=![]() ;
;
②12+22+32+…+n2=![]() ,其中n为正整数)
,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.
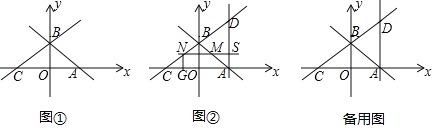
(1)求直线BC的解析式.
(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒![]() 个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
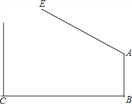
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).

(1)OB=_________,抛物线的顶点坐标为_________________;
(2)当n=4时,求点P关于直线BC的对称点P′的坐标;
(3)是否存在直线PD,使直线PD所对应的一次函数随x的增大而增大?若存在,直接写出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com