
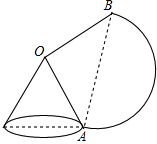
 如图,沿OA将圆锥侧面剪开,展开成平面图形后是扇形OAB.
如图,沿OA将圆锥侧面剪开,展开成平面图形后是扇形OAB. 解:(1)扇形的弧长等于其围成的圆锥的底面周长,点A与点B在圆锥的侧面上重合;
解:(1)扇形的弧长等于其围成的圆锥的底面周长,点A与点B在圆锥的侧面上重合;| 90πR |
| 180 |
|
| ||
| 2 |
| 90πr2 |
| 360 |
| 2 |


科目:初中数学 来源: 题型:
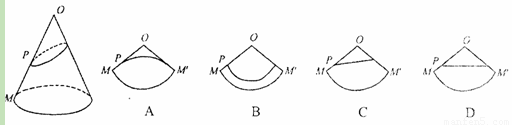
 4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )
4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )查看答案和解析>>
科目:初中数学 来源:新课程同步练习 数学 八年级下册 人教版 题型:038
如图,沿OA将圆锥侧面剪开,展开成平面图形是扇形OAB.
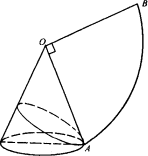
(1)扇形的弧AB的长与圆锥底面圆周的长是怎样的关系?点A和点B在圆锥的侧面上是怎样的位置关系?
(2)若∠AOB=90°,占A在圆锥侧面上运动一圈后又回到原位,则点A运动的最短路程应怎样设计(设底面圆半径为r)?若r=![]() 且∠AOB=90°,求点A运动的最短路程.
且∠AOB=90°,求点A运动的最短路程.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广东肇庆卷)数学 题型:选择题
己知O为圆锥的顶点,M 为圆锥底面上一点,点 P 在 OM上.一只锅牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示,若沿OM将圆锥侧面剪开并展开,所得侧面展开图是
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,沿OA将圆锥侧面剪开,展开成平面图形后是扇形OAB.
如图,沿OA将圆锥侧面剪开,展开成平面图形后是扇形OAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com