
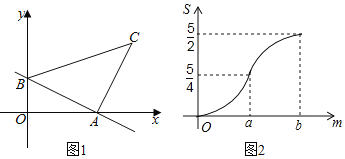
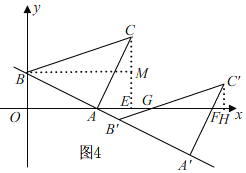
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпABгыxжсЁЂyжсЗжБ№ЯрНЛгкЕуAЁЂBЃЌНЋЯпЖЮABШЦЕуAЫГЪБеыа§зЊ90ЁуЃЌЕУЕНACЃЌСЌНгBCЃЌНЋЁїABCбиЩфЯпBAЦНвЦЃЌЕБЕуCЕНДяxжсЪБдЫЖЏЭЃжЙЃЎЩшЦНвЦОрРыЮЊmЃЌЦНвЦКѓЕФЭМаЮдкxжсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌSЙигкmЕФКЏЪ§ЭМЯѓШчЭМ2ЫљЪОЃЈЦфжа0ЃМmЁмaЃЌaЃМmЁмbЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉЃЎ
ЃЈ1ЃЉЬюПеЃКЁїABCЕФУцЛ§ЮЊ ЃЛ
ЃЈ2ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЧѓSЙигкmЕФНтЮіЪНЃЌВЂаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉжБЯпABЕФНтЮіЪНЮЊy=Љ
ЃЛЃЈ2ЃЉжБЯпABЕФНтЮіЪНЮЊy=Љ![]() x+1ЃЛЃЈ3ЃЉS=
x+1ЃЛЃЈ3ЃЉS=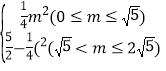 ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉгЩЭМ2НсКЯЦНвЦМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉХаЖЯГіЁїAOBЁеЁїCEAЃЌЕУГіAEЃНOBЃЌCEЃНOAЃЌдйгЩЭМ2жЊЃЌЕуCЕФзнзјБъЪЧЕуBзнзјБъЕФ2БЖЃЌМДПЩРћгУШ§НЧаЮABCЕФУцЛ§ЧѓГіOBЃЌOAЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃЌРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЛђШ§НЧаЮЕФУцЛ§ВюМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉНсКЯЁїABCЕФвЦЖЏКЭЭМ2жЊЃЌЕуBвЦЖЏЕНЕуAДІЃЌОЭЪЧЭМ2жаЃЌm=aЪБЃЌS=SЁїA'B'D=![]() ЃЌЕуCвЦЖЏЕНxжсЩЯЪБЃЌМДЃКm=bЪБЃЌS=SЁїA'B'C'=SЁїABC=
ЃЌЕуCвЦЖЏЕНxжсЩЯЪБЃЌМДЃКm=bЪБЃЌS=SЁїA'B'C'=SЁїABC=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуCзїCEЁЭxжсгкEЃЌ
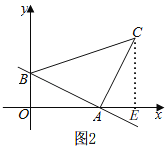
ЁрЁЯAEC=ЁЯBOA=90ЁуЃЎ
ЁпЁЯBAC=90ЁуЃЌ
ЁрЁЯOAB+ЁЯCAE=90ЁуЃЌ
ЁпЁЯOAB+ЁЯOBA=90ЁуЃЌ
ЁрЁЯOBA=ЁЯCAEЃЌ
гЩа§зЊжЊЃЌAB=ACЃЌ
ЁрЁїAOBЁеЁїCEAЃЌ
ЁрAE=OBЃЌCE=OAЃЌ
гЩЭМ2жЊЃЌЕуCЕФзнзјБъЪЧЕуBзнзјБъЕФ2БЖЃЌ
ЁрOA=2OBЃЌ
ЁрAB2=5OB2ЃЌ
гЩЃЈ1ЃЉжЊЃЌSЁїABC=![]() =
=![]() AB2=
AB2=![]() ЁС5OB2ЃЌ
ЁС5OB2ЃЌ
ЁрOB=1ЃЌ
ЁрOA=2ЃЌ
ЁрAЃЈ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ1ЃЉЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊy=Љ![]() x+1ЃЛ
x+1ЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌAB2=5ЃЌ
ЁрAB=![]() ЃЌ
ЃЌ
ЂйЕБ0ЁмmЁм![]() ЪБЃЌШчЭМ3ЃЌ
ЪБЃЌШчЭМ3ЃЌ
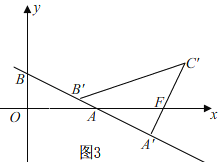
ЁпЁЯAOB=ЁЯAA'FЃЌЁЯOAB=ЁЯA'AFЃЌ
ЁрЁїAOBЁзЁїAA'FЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩдЫЖЏжЊЃЌAA'=mЃЌЁр![]() ЃЌ
ЃЌ
ЁрA'F=![]() mЃЌ
mЃЌ
ЁрS=![]() AA'ЁСA'F=
AA'ЁСA'F=![]() m2ЃЌ
m2ЃЌ
ЂкЕБ![]() ЃМmЁм2
ЃМmЁм2![]() ЪБЃЌШчЭМ4ЃЌ
ЪБЃЌШчЭМ4ЃЌ
ЭЌЂйЕФЗНЗЈЕУЃКA'F=![]() mЃЌ
mЃЌ
ЁрC'F=![]() Љ
Љ![]() mЃЌ
mЃЌ
Й§ЕуCзїCEЁЭxжсгкEЃЌЙ§ЕуBзїBMЁЭCEгкEЃЌ
ЁрBM=3ЃЌCM=1ЃЌ
взжЊЃЌЁїACEЁзЁїFC'HЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрC'H=![]() ЃЎ
ЃЎ
дкRtЁїFHC'жаЃЌFH=![]() C'H=
C'H=![]() ЃЌ
ЃЌ
гЩЦНвЦжЊЃЌЁЯC'GF=ЁЯCBMЃЌ
ЁпЁЯBMC=ЁЯGHC'ЃЌ
ЁрЁїBMCЁзЁїGHC'ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрGH=![]() ЃЌ
ЃЌ
ЁрGF=GHЉFH=![]() ЃЌ
ЃЌ
ЁрS=SЁїA'B'C'ЉSЁїC'FG=![]() Љ
Љ![]() ЁС
ЁС![]() ЁС
ЁС![]() =
=![]() Љ
Љ![]() ЃЈ2
ЃЈ2![]() ЉmЃЉ2ЃЌ
ЉmЃЉ2ЃЌ
МДЃКS= ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() ЁЂ
ЁЂ![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЪЧ
ЕФзјБъЪЧ![]() ЃЌ
ЃЌ
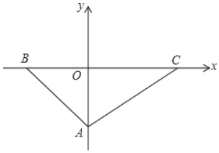
ЃЈ1ЃЉЧѓ![]() Ш§ИіЖЅЕу
Ш§ИіЖЅЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉСЌНг![]() ЁЂ
ЁЂ![]() ЃЌВЂгУКЌзжФИ
ЃЌВЂгУКЌзжФИ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ЕФУцЛ§ЃЈ
ЕФУцЛ§ЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЮЪЕФЬѕМўЯТЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЃПШчЙћДцдкЃЌЧыЧѓГіЕу
ЕФУцЛ§ЃПШчЙћДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСаЗНГЬЃЈзщЃЉЛђВЛЕШЪНЃЈзщЃЉНтгІгУЬтЃК
ЃЈ1ЃЉМзЙЄШЫНгЕН240ИіСуМўЕФШЮЮёЃЌЙЄзї1аЁЪБКѓЃЌвђвЊЬсЧАЭъГЩШЮЮёЃЌЕїРДввКЭМзКЯзїЃЌКЯзіСЫ5аЁЪБЭъГЩ.вбжЊМзУПаЁЪББШввЩйзі4ИіЃЌФЧУДМзЁЂввУПаЁЪБИїзіЖрЩйИіЃП
ЃЈ2ЃЉФГЙЄГЇзМБИЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛњЦїЙВ20ЬЈгУгкЩњВњСуМўЃЌОЕїВщ2ЬЈ
СНжжЛњЦїЙВ20ЬЈгУгкЩњВњСуМўЃЌОЕїВщ2ЬЈ![]() аЭЛњЦїКЭ1ЬЈ
аЭЛњЦїКЭ1ЬЈ![]() аЭЛњЦїМлИёЮЊ18ЭђдЊЃЌ1ЬЈ
аЭЛњЦїМлИёЮЊ18ЭђдЊЃЌ1ЬЈ![]() аЭЛњЦїКЭ2ЬЈ
аЭЛњЦїКЭ2ЬЈ![]() аЭЛњЦїМлИёЮЊ21ЭђдЊ.
аЭЛњЦїМлИёЮЊ21ЭђдЊ.
ЂйЧѓвЛЬЈ![]() аЭЛњЦїКЭвЛЬЈ
аЭЛњЦїКЭвЛЬЈ![]() аЭЛњЦїМлИёЗжБ№ЪЧЖрЩйЭђдЊЃП
аЭЛњЦїМлИёЗжБ№ЪЧЖрЩйЭђдЊЃП
ЂквбжЊ1ЬЈ![]() аЭЛњЦїУПдТПЩМгЙЄСуМў400ИіЃЌ1ЬЈ
аЭЛњЦїУПдТПЩМгЙЄСуМў400ИіЃЌ1ЬЈ![]() аЭЛњЦїУПдТПЩМгЙЄСуМў800ИіЃЌОдЄЫуЙКТђСНжжЛњЦїЕФМлИёВЛГЌЙ§140ЭђдЊЃЌУПдТСНжжЛњЦїМгЙЄСуМўзмЪ§ВЛЕЭгк12400ИіЃЌФЧУДгаФФМИжжЙКТђЗНАИЃЌФФжжЗНАИзюЪЁЧЎЃП
аЭЛњЦїУПдТПЩМгЙЄСуМў800ИіЃЌОдЄЫуЙКТђСНжжЛњЦїЕФМлИёВЛГЌЙ§140ЭђдЊЃЌУПдТСНжжЛњЦїМгЙЄСуМўзмЪ§ВЛЕЭгк12400ИіЃЌФЧУДгаФФМИжжЙКТђЗНАИЃЌФФжжЗНАИзюЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЭBCЧвAB=BCЃЌDEЁЭCDЧвDE=CDЃЌЧыАДееЭМжаЫљБъзЂЕФЪ§ОнЃЌМЦЫуЭМжаЪЕЯпЫљЮЇГЩЕФЭМаЮЕФУцЛ§SЪЧЃЈ ЃЉ

A. 36B. 48C. 72D. 108
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњзюЯВЛЖЕФЧђРрдЫЖЏЧщПіЃЌЫцЛњбЁШЁИУаЃВПЗжбЇЩњНјааЕїВщЃЌвЊЧѓУПУћбЇЩњжЛаДвЛРрзюЯВЛЖЕФЧђРрдЫЖЏЃЎвдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЎ
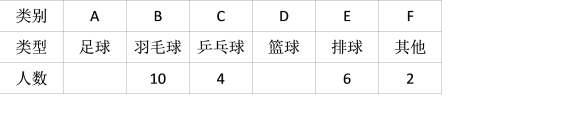
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБЛЕїВщЕФбЇЩњжаЃЌзюЯВЛЖЦЙХвЧђЕФга ШЫЃЌзюЯВЛЖРКЧђЕФбЇЩњЪ§еМБЛЕїВщзмШЫЪ§ЕФАйЗжБШЮЊ %ЃЛ
ЃЈ2ЃЉБЛЕїВщбЇЩњЕФзмЪ§ЮЊ ШЫЃЌЦфжаЃЌзюЯВЛЖРКЧђЕФга ШЫЃЌзюЯВЛЖзуЧђЕФбЇЩњЪ§еМБЛЕїВщзмШЫЪ§ЕФАйЗжБШЮЊ %ЃЛ
ЃЈ3ЃЉИУаЃЙВга450УћбЇЩњЃЌИљОнЕїВщНсЙћЃЌЙРМЦИУаЃзюЯВЛЖХХЧђЕФбЇЩњЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШБпШ§НЧаЮ![]() жа
жа![]() Еу
Еу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌЕу
БпЩЯЕФвЛЕуЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌСЌНг
БпЩЯЕФвЛЕуЃЌСЌНг![]() вд
вд![]() ЮЊБпзїЕШБпШ§НЧаЮ
ЮЊБпзїЕШБпШ§НЧаЮ![]() СЌНг
СЌНг![]() ЃЎ
ЃЎ
![]() ШчЭМ1ЃЌЕБЕу
ШчЭМ1ЃЌЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ
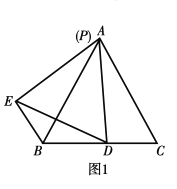
![]() евГіЭМжаЕФвЛЖдШЋЕШШ§НЧаЮЃЌВЂжЄУїЃЛ
евГіЭМжаЕФвЛЖдШЋЕШШ§НЧаЮЃЌВЂжЄУїЃЛ
![]() ЃЛ
ЃЛ
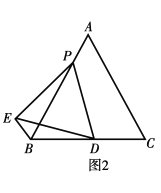
![]() ШчЭМ2ЃЌШє
ШчЭМ2ЃЌШє![]() ЧыМЦЫу
ЧыМЦЫу![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOЮЊЁїABCЕФСНЬѕНЧЦНЗжЯпЕФНЛЕуЃЌЙ§ЕуOзїODЁЭBCгкЕуDЃЌЧвODЃН4ЃЎШєЁїABCЕФжмГЄЪЧ17ЃЌдђЁїABCЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A. 34B. 17C. 8.5D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
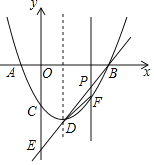
ЁОЬтФПЁПШчЭМЃЌЖдГЦжсЮЊжБЯпx=1ЕФХзЮяЯпy=x2Љbx+cгыxжсНЛгкAЃЈx1ЃЌ0ЃЉЁЂBЃЈx2ЃЌ0ЃЉЃЈx1ЃМx2ЃЉСНЕуЃЌгыyжсНЛгкCЕуЃЌЧв![]() +
+![]() =Љ
=Љ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпЖЅЕуЮЊDЃЌжБЯпBDНЛyжсгкEЕуЃЛ
ЂйЩшЕуPЮЊЯпЖЮBDЩЯвЛЕуЃЈЕуPВЛгыBЁЂDСНЕужиКЯЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпгыХзЮяЯпНЛгкЕуFЃЌЧѓЁїBDFУцЛ§ЕФзюДѓжЕЃЛ
ЂкдкЯпЖЮBDЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУЁЯBDC=ЁЯQCEЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЯТСаИїЪ§ЬюШыЫќЫљдкЕФЪ§МЏЕФРЈКХРяЃЎ
Љ![]() ЃЌ+5ЃЌЉ6.3ЃЌ0ЃЌЉ
ЃЌ+5ЃЌЉ6.3ЃЌ0ЃЌЉ![]() ЃЌ2
ЃЌ2![]() ЃЌ6.9ЃЌЉ7ЃЌ210ЃЌ0.031ЃЌЉ43ЃЌЉ10%
ЃЌ6.9ЃЌЉ7ЃЌ210ЃЌ0.031ЃЌЉ43ЃЌЉ10%
е§Ъ§МЏКЯЃК{ЁЁ ЁЁЁ}
ећЪ§МЏКЯЃК{ЁЁ ЁЁЁ}
ЗЧИКЪ§МЏКЯЃК{ЁЁ ЁЁЁ}
ИКЗжЪ§МЏКЯЃК{ЁЁ ЁЁЁ}ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com