
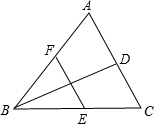
 如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.  智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x(3x2y-2xy)=-6x2y-4x2y | B. | 2x2y(-x2+2y+1)=-4x3y4 | ||
| C. | (3ab2-2ab)abc=3a2b2-2a2b2 | D. | (ab)2(2ab2c)=2a3b4c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段/分 | 组中值 | 频数(人数) | 频率 |
| 60≤x<70 | 65 | 30 | 0.15 |
| 70≤x<80 | 75 | b | 0.45 |
| 80≤x<90 | 85 | 60 | c |
| 90≤x<100 | a | 20 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com