
【题目】问题提出:如果一个多边形的各个顶点均在另一个多边形的边上,则称这个多边形为另一多边形的内接多边形
问题探究:
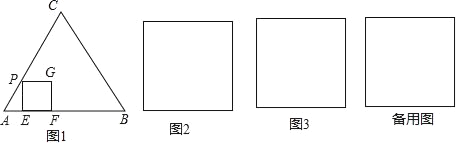
(1)如图1,正方形PEFG的顶点E、F在等边三角形ABC的边AB上,顶点P在AC边上.请在等边三角形ABC内部,以A为位似中心,作出正方形PEFG的位似正方形P'E'F'G',且使正方形P'E'F'G'的面积最大(不写作法)
(2)如图2,在边长为4正方形ABCD中,画出一个面积最大的内接正三角形,并求此最大内接正三角形的面积
拓展应用:
(3)如图3,在边长为4的正方形ABCD中,能不能截下一个面积最大的直角三角形,并使其三边比为3:4:5,若能,请求出此直角三角形的最大面积,若不能,请说明理由.
【答案】(1)详见解析;(2)S△DEF=16(2![]() ﹣3);(3)能,S△DEF=
﹣3);(3)能,S△DEF=![]() .
.
【解析】
(1)利用位似图形的性质,作出正方形PEFG的位似正方形P'E'F'G',如图1所示;
(2)如图2,△DEF是最大内接正三角形,在AD上取一点M,使得EM=MD.由△DAE≌△DCF,推出∠ADE=∠CDF,由∠ADC=90°,推出∠ADE=∠CDF=15°,推出∠MED=∠MDE=15°,推出∠AME=∠MED+∠MDE=30°,设AE=a,则EM=DM=2a,AM=![]() a,可得
a,可得![]() a+2a=4,推出a=4(2-
a+2a=4,推出a=4(2-![]() ),推出BE=BF=4(
),推出BE=BF=4(![]() -1),由此即可解决问题.
-1),由此即可解决问题.
(3)能.理由:如图3中,假设△BEF是直角三角形,EF:BE:BF=3:4:5,由△ABE∽△DEF,可得![]() ,AB=4,推出DE=3,AE=1,DF=
,AB=4,推出DE=3,AE=1,DF=![]() ,推出BE=
,推出BE=![]() ,EF=
,EF=![]() ,BF=
,BF=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)如图1,正方形P'E'F'G'即为所求;
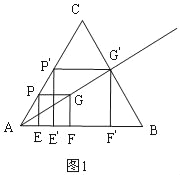
(2)如图2,△DEF是最大内接正三角形,在AD上取一点M,使得EM=MD.
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
在Rt△DAE和Rt△DCF中,
![]() ,
,
∴△DAE≌△DCF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠ADE=∠CDF=15°,
∴∠MED=∠MDE=15°,
∴∠AME=∠MED+∠MDE=30°,
设AE=a,则EM=DM=2a,AM=![]() a,
a,
∴![]() a+2a=4,
a+2a=4,
∴a=4(2﹣![]() ),
),
∴BE=BF=4(![]() ﹣1),
﹣1),
∴S△DEF=16﹣2×![]() ×4×4(2﹣
×4×4(2﹣![]() )﹣
)﹣![]() ×4(
×4(![]() ﹣1)×4(
﹣1)×4(![]() ﹣1)=16(2
﹣1)=16(2![]() ﹣3).
﹣3).
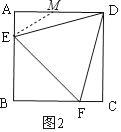
(3)能.理由:如图3中,假设△BEF是直角三角形,EF:BE:BF=3:4:5,
∵∠A=∠D=∠BEF=90°,
∴∠AEB+∠ABE=90°,∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF,
∴![]() ,
,
∵AB=4,
∴DE=3,AE=1,DF=![]() ,
,
∴BE=![]() ,EF=
,EF=![]() ,BF=
,BF=![]() ,
,
∴△BEF满足条件,
∴S△DEF=![]() BEEF=
BEEF=![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
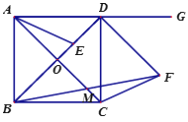
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
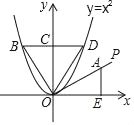
【题目】如图,射线OP与x轴正半轴的夹角为30°,点A是OP上一点,过点A作x轴的垂线与x轴交于点E.△AOE绕着点O逆时针旋转90°后能与△BOC重合,△BOC沿着y轴翻折能与△DOC重合,若点D恰好在抛物线y=x2(x>0)上,则点A的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
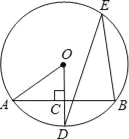
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
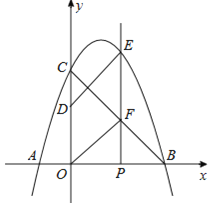
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com