
【题目】阅读下列各题并按要求完成:
(1)定义:若两个一元二次方程有一个相同的实数根,则称这两个方程为“友好方程”,已知关于x的一元二次方程 x 2x 0 与 x 3x m 1 0 为“友好方程”,求 m 的值;
(2)关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,且二次根式
,且二次根式![]() 有意义,若T=
有意义,若T=![]() ,求T的取值范围;
,求T的取值范围;
(3)我们不妨约定方程的整数解称之为“硬核”,例如x=1就称为方程(x-1)(2x+1)=0 的一个“硬核”,若一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0(k为常数)有两个不同的“硬核”,试确定方程的两个“硬核”及常数 k 的值.
【答案】(1)9或1;(2)![]() ;(3)方程的两个“硬核”为3和1,k=
;(3)方程的两个“硬核”为3和1,k=![]() .
.
【解析】
(1)首先解第一个方程,然后利用友好方程的定义代入第二个方程求得m的值即可;
(2)首先根据一元二次方程有两个不相等的实数根和二次根式有意义的条件,得到关于m的不等式,求出m的取值范围,然后对T进行化简,代入x1+x2=4-2m,x1x2= m2-3m+3,可得![]() ,最后由m的取值范围可得T的取值范围;
,最后由m的取值范围可得T的取值范围;
(3)由方程为一元二次方程即可得出k-3k+2≠0,解之可得出k≠1且k≠2,利用因式分解法解一元二次方程可得出x1=![]() ,x2=
,x2=![]() ,由方程的两根均为整数可设
,由方程的两根均为整数可设![]() ,
,![]() (其中m、n均是不为1的整数),分析得出k≠0,n≠0,解分式方程用含m、n的代数式表示出k值,得到m=2
(其中m、n均是不为1的整数),分析得出k≠0,n≠0,解分式方程用含m、n的代数式表示出k值,得到m=2![]() ,结合m、n均为整数即可求出n=1,然后易求m与k值,此题得解.
,结合m、n均为整数即可求出n=1,然后易求m与k值,此题得解.
解:(1)解x22x=0得:x=0或x=2,
∵关于x的一元二次方程x22x=0与x2+3x+m1=0为“友好方程”,
∴22+3×2+m1=0或02+3×0+m1=0,
解得:m=9或m=1,
∴m的值为9或1;
(2)∵关于x的一元二次方程![]() 有两个不相等的实数根,
有两个不相等的实数根,
∴△=[2(m-2)]2-4(m2-3m+3)>0,x1+x2=4-2m,x1x2= m2-3m+3,
∵二次根式![]() 有意义,
有意义,
∴m+1≥0,
∴-1≤m<1,
∴T=![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴![]() ,即
,即![]() ;
;
(3)∵方程(k-3k+2)x+(2k-4k+1)x+k-k=0为一元二次方程,
∴k-3k+2=(k1)(k2)≠0,
∴k≠1且k≠2.
∵(k-3k+2)x+(2k-4k+1)x+k-k=[(k1)x+k][(k2)x+k1]=0,
∴x1=![]() ,x2=
,x2=![]() ,
,
∵一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0有两个不相等的整数解,
∴设![]() ,
,![]() (其中m、n均是不为1的整数),
(其中m、n均是不为1的整数),
∵当k=0时,x1=0,x2=![]() ,
,
∴k≠0,
∵k≠1,
∴n≠0.
∴k=![]() =
=![]() ,
,
∴m=2![]() .
.
∵m为整数,n为整数,
∴n=1或n=1(舍去).
∴![]() ,m=2
,m=2![]() =3,
=3,
解得:k=![]() .
.
即方程的两个“硬核”为3和1,k=![]() .
.


科目:初中数学 来源: 题型:
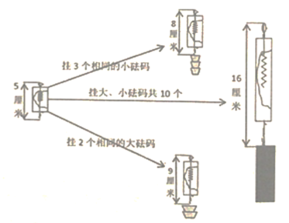
【题目】我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 ![]() ,挂一个大砝码弹簧伸长
,挂一个大砝码弹簧伸长 ![]() .
.
(2)如果要使弹簧长度为![]() ,应挂大砝码、小砝码各多少个?
,应挂大砝码、小砝码各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的精神生活美化城市环境,城市管理局从外地新进一批绿化树苗,现有两种运输方式可供选择,
方式一:使用快递公司的邮车运输,装卸收费500元,另外每公里再加收5元;
方式二:使用铁路运输公司的火车运输,装卸收费900元,另外每公里再加收3元.
(1)请分别写出邮车、火车运输的总费用为![]() (元)、
(元)、![]() (元)与运输路程
(元)与运输路程![]() (公里)之间的函数关系式;
(公里)之间的函数关系式;
(2)你认为选用哪种运输方式较好,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
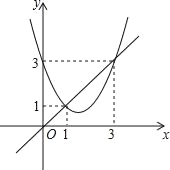
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两点在同一条数轴上,点A在原点的左边,到原点的距离为4,点B在原点右边,点A 到B点的距离为16.
(1)求A,B两点所表示的数:
(2)若A,B两点分别以每秒1个单位长度和3个单位长度的速度同时相向移动,在点C相遇,求点C表示的数?
查看答案和解析>>
科目:初中数学 来源: 题型:
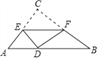
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
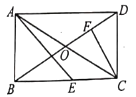
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com