
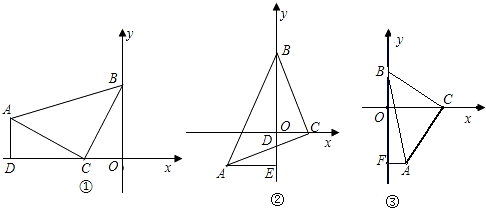
���� ��1��ֻҪ���Rt��ADC��Rt��COB������
��2����˵��BD��AE��������������ϵ��Ȼ����Եõ���������ϵ���������ʵĸ����ߣ�������Ӧ��ͼ�Σ����ݵ��������εױ��ϵĸߡ��ױ��ϵ����ߡ����ǵ�ƽ�������ߺ�һ����������֤����Ҫ˵����������ϵ��
��3���Ȳ���OC��AF��OB֮��Ĺ�ϵ��Ȼ����ݲ����������ʵĸ����ߣ�������Ӧ��ͼ�Σ�Ȼ��֤����Ҫ֤���Ľ��ۼ��ɣ�
��� �⣺��1���ߵ�C�����ǣ�-1��0������A�������ǣ�-3��1��
��AD=OC��
��Rt��ADC��Rt��COB��
$\left\{\begin{array}{l}{AD=OC}\\{AC=BC}\end{array}\right.$��
��Rt��ADC��Rt��COB��HL����
��OB=CD=2��
���B�������ǣ�0��2����
��2��BD=2AF��
���ɣ���AE���ӳ��߽�BC���ӳ����ڵ�F������ͼ2��ʾ��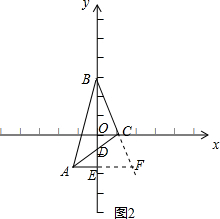
�ߡ�ABC�ǵ���ֱ�������Σ�BC=AC��ֱ�Ƕ���C��x���ϣ�AE��y����E��
���BCA=��ACF=90�㣬��AED=90�㣬
���DBC+��BDC=90�㣬��DAE+��ADE=90�㣬
�ߡ�BDC=��ADE��
���DBC=��FAC��
�ڡ�BDC�͡�AFC�У�
$\left\{\begin{array}{l}{��BCD=��ACF}\\{BC=AC}\\{��DBC=��FAC}\end{array}\right.$��
���BDC�ա�AFC��ASA��
��BD=AF��
��BE��AE��y��ǡ��ƽ�֡�ABC��
��AF=2AE��
��BD=2AF��
��3��OC=OB+AF��
֤������AE��OC�ڵ�E������ͼ3��ʾ��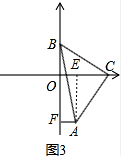
��AE��OC��AF��y�ᣬ
���ı���OFAE�Ǿ��Σ���AEC=90�㣬
��AF=OE��
�ߡ�ABC�ǵ���ֱ�������Σ�BC=AC��ֱ�Ƕ���C��x���ϣ���BOC=90�㣬
���BCA=90�㣬
���BCO+��CBO=90�㣬��BCO+��ACE=90�㣬
���CBO=��ACE��
�ڡ�BOC�͡�CEO�У�
$\left\{\begin{array}{l}{��BOC=��CEA}\\{��CBO=��ACE}\\{BC=AC}\end{array}\right.$
���BOC�ա�CEO��AAS��
��OB=CE��
��OC=OE+EC��OE=AF��OB=EC��
��OC=OB+AF��
���� ���⿼��ȫ�������ε��ж������ʡ�������ͼ�ε����ʡ�����ֱ�������Σ�����Ĺؼ�����ȷ���⣬�������ʵĸ����ߣ��ҳ�����������Ҫ���������������ν�ϵ�˼�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
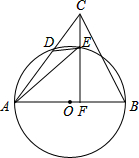 ��ͼ���ڡ�ABC�У�AB�ǡ�O��ֱ����AC���O���ڵ�D����E��$\widehat{BD}$�ϣ�����DE��AE������CE���ӳ���AB�ڵ�F����AED=��ACF��
��ͼ���ڡ�ABC�У�AB�ǡ�O��ֱ����AC���O���ڵ�D����E��$\widehat{BD}$�ϣ�����DE��AE������CE���ӳ���AB�ڵ�F����AED=��ACF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
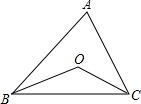 ��֪�ڡ�ABC�У���A=62�㣬BO��CO�ֱ��ǡ�ABC����ACB��ƽ���ߣ���BO��CO�ཻ��O�����BOC�Ķ�����121�㣮
��֪�ڡ�ABC�У���A=62�㣬BO��CO�ֱ��ǡ�ABC����ACB��ƽ���ߣ���BO��CO�ཻ��O�����BOC�Ķ�����121�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 28 | C�� | -28 | D�� | -18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3{a}^{4}{b}^{2}}{6{a}^{2}{b}^{4}}$=$\frac{{a}^{3}}{2{b}^{2}}$ | B�� | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | ||
| C�� | $\frac{x+3}{{x}^{2}-9}$=$\frac{3}{x-3}$ | D�� | $\frac{b-a}{��a-b��^{2}}$=$\frac{1}{b-a}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com