
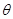 为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为 ▲ .
为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为 ▲ .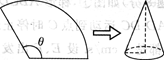
科目:初中数学 来源:不详 题型:解答题
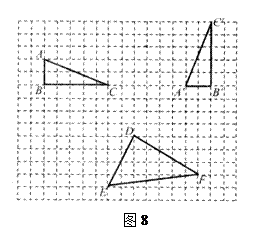
 是由格点
是由格点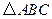 通过怎样变换得到的?
通过怎样变换得到的?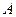 的坐标为(
的坐标为(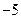 ,
,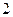 ),点
),点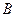 的坐标为
的坐标为 ,请求出过
,请求出过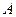 点的正比例函数的解析式,并写出图中格点
点的正比例函数的解析式,并写出图中格点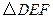 各顶点的坐标.
各顶点的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,点F在边BC上,E在边BA的延长线上,
中,点F在边BC上,E在边BA的延长线上, 按顺时针方向旋转后能与
按顺时针方向旋转后能与 重合.
重合.
 ,求四边形
,求四边形 的面积.
的面积. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
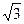 时,求菱形BNDM的面积.
时,求菱形BNDM的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
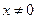 ),则AP="2x" cm,CM="3x" cm,DN="x2" cm.
),则AP="2x" cm,CM="3x" cm,DN="x2" cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com