
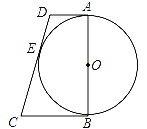
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
【答案】(1)答案见解析;(2)4.
【解析】试题分析:(1)证明△OBC≌△OEC,得出∠OBC=∠OEC=90°,证出BC为⊙O的切线;
(2)过点D作DF⊥BC于F,求出DF=AB=4,BF=AD=1,设CE=x,Rt△CDF中,根据勾股定理得出x的值即可.
试题解析:(1)连接OE,OC;如图所示:∵DE与⊙O相切于点E,∴∠OEC=90°,在△OBC和△OEC中,∵OB=OE,CB=CE,OC=OC,∴△OBC≌△OEC(SSS),∴∠OBC=∠OEC=90°,∴BC为⊙O的切线;
(2)过点D作DF⊥BC于F;如图所示:设CE=x,∵CE,CB为⊙O切线,∴CB=CE=x,∵DE,DA为⊙O切线,∴DE=DA=1,∴DC=x+1,∵∠DAB=∠ABC=∠DFB=90°,∴四边形ADFB为矩形,∴DF="AB=4" BF=AD=1,∴FC=x﹣1,Rt△CDF中,根据勾股定理得:![]() ,解得:x=4,∴CE=4.
,解得:x=4,∴CE=4.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=![]() ,∠ABC=
,∠ABC=![]() ,∠BCA=
,∠BCA=![]() ,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
,△ABC的三条角平分线AD,BE,CF交于点O,过O向△ABC三边作垂线,垂足分别为P,Q,H,如下图所示。
(1)若![]() =78°,
=78°,![]() =56°,
=56°,![]() =46°,求∠EOH的大小;
=46°,求∠EOH的大小;
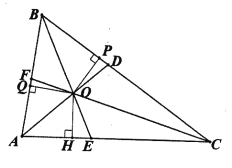
(2)用![]() ,
,![]() ,
,![]() 表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
表示∠EOH的表达式为∠EOH= ;(要求表达式最简)
(3)若![]() ≥
≥![]() ≥
≥![]() ,∠EOH+∠DOP+∠FOQ=
,∠EOH+∠DOP+∠FOQ=![]() ,判断△ABC的形状并说明理由。
,判断△ABC的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“母亲节”快到了,七(1)班班委发起慰问烈士家属王大妈和李大妈的活动,决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集资金.已知同学们从花店按每枝1.4元买进鲜花,并按每枝3元卖出,设卖出鲜花x枝.
品名 | 热水壶 | 电饭煲 |
单价(单位:元/只) | 125 | 250 |
(1)每卖出一枝鲜花赚_______元,卖出鲜花x枝赚______元;
(2)若从花店购买鲜花的同时,同学们还花了50元购买包装材料,请把所筹集的资金y(元)用鲜花的销售量x(枝)的代数式表示;现在筹集的资金为750元,问需要卖出鲜花多少枝?
(3)已知两种家用小电器的单价如下表所示,现将筹集的750元全部用于购买表中家用小电器赠送两位大妈,且电饭煲至少要购买1只,请求出所有的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,DE∥BC,∠1 = ∠3 ,请说明 FG ∥ DC ;
(2)若把题设中 DE ∥ BC 与结论中 FG ∥ DC 对调,命题还成立吗?试证明。
(3)若把题设中∠1=∠3 与结论中 FG ∥ DC 对调呢?试证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区要调查社区居民双休日的学习状况,采用下列调查方式:

①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
(1)上述调查方式最合理的是 ;
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2),在这个调查中,200名居民双休日在家学习的有 人;
(3)请估计该社区2 000名居民双休日学习时间不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
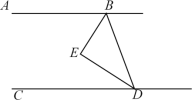
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC。
(1)求证:BE⊥DE;
(2)H是直线CD上一动点(不与D重合),HI平分∠HBD交CD于点I。请你画出图形,并猜想∠EBI与∠BHD的数量关系,且说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
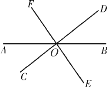
【题目】如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,∠AOC的邻补角是_______.若∠AOC=50°,则∠BOD=__________,∠COB=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com