
【题目】如图1,抛物线y=﹣x2﹣2x+3与x轴从左到右交于A、B两点,与y轴交于点C,顶点为D

(1)求直线AC的解析式与点D的坐标;
(2)在直线AC上方的抛物线上有一点E,作EF∥x轴,与抛物线交于点F,作EM⊥x轴于M,作FN⊥x轴于N,长度为2![]() 的线段PQ在直线AC上运动(点P在点Q右侧),当四边形EMNF的周长取最大值求四边形DPQE的周长的最小值及对应的点Q的坐标;
的线段PQ在直线AC上运动(点P在点Q右侧),当四边形EMNF的周长取最大值求四边形DPQE的周长的最小值及对应的点Q的坐标;
(3)如图2,平移抛物线,使抛物线的顶点D在直线AD上移动,点D平移后的对应点为D′,点A平移后的对应点为A′,△A′D′C是否能为直角三角形?若能,请求出对应的线段D′C的长;若不能,请说明理由.
【答案】(1)直线AC的解析式为:![]() ,
,![]() ;(2)四边形DPQE的周长的最小值是
;(2)四边形DPQE的周长的最小值是![]() ,对应的点Q的坐标为
,对应的点Q的坐标为![]() ;(3)
;(3)![]() =
=![]() 或
或![]() 或3.
或3.
【解析】
(1)抛物线![]() 与x轴从左到右交于A、B两点,只要令y=0,即可求出A、B两点;与y轴交于点C,只要令x=0,即可求出点C;由点A、C的坐标可得直线AC的解析;D的坐标用顶点公式或者先求出对称轴代入解析式,即可求出;
与x轴从左到右交于A、B两点,只要令y=0,即可求出A、B两点;与y轴交于点C,只要令x=0,即可求出点C;由点A、C的坐标可得直线AC的解析;D的坐标用顶点公式或者先求出对称轴代入解析式,即可求出;
(2)作点E关于直线AC的对称点E'(0,1),将点E'沿AC方向平移![]() 个单位得到E″(2,3),连接E″D交直线AC于点P,将点P向下平移
个单位得到E″(2,3),连接E″D交直线AC于点P,将点P向下平移![]() 个单位得到Q,则点Q为所求点即可求解,再根据个点坐标求出四边形的边长,进而计算周长;
个单位得到Q,则点Q为所求点即可求解,再根据个点坐标求出四边形的边长,进而计算周长;
(3)分A'D'是斜边、A'C是斜边、CD'是斜边三种情况,分别求解即可.
解:(1)∵抛物线![]() 与x轴从左到右交于A、B两点,
与x轴从左到右交于A、B两点,
∴令y=0,即![]() ,解得:
,解得:![]() ,则
,则![]()
∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴![]()
由点A、C的坐标得,直线AC的解析式为:![]() ;
;
∵D是抛物线![]() 的顶点,抛物线的对称轴为:
的顶点,抛物线的对称轴为:![]() ,
,
∴![]() ;
;
(2)设点![]() ,
,
∵抛物线的对称轴为:![]() ,
,![]() 轴,
轴,
∴![]()
四边形![]() 的周长
的周长![]() ,
,
当![]() 时,
时,![]() 最大,此时点
最大,此时点![]() ;
;
∵![]() ,
,![]() ;
;
∴![]() ;
;
∵![]() 且P、Q在
且P、Q在![]() 上
上
∴P、Q两点横纵坐标差为2,
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,将点
,将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,
,
由点![]() 坐标得,直线
坐标得,直线![]() 的解析式为:
的解析式为:![]() ;
;
联立直线AC、直线![]() 的解析式并解得:
的解析式并解得:![]() ,故点
,故点![]() ,
,
将点![]() 沿着直线CA向左向下平移
沿着直线CA向左向下平移![]() 个单位得到点
个单位得到点![]() ;
;
∵![]() ,
,![]() ,
,![]() ,
,![]() ;
;
∴![]() ,
,![]() ;
;
此时四边形![]() 的周长最小
的周长最小
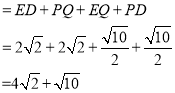 ;
;
(3)由待定系数法求得直线AD的解析式为:![]() ,则设抛物线向右平移m个单位,则向上平移2m个单位,
,则设抛物线向右平移m个单位,则向上平移2m个单位,
∴![]()
![]() 、
、![]()
![]() ,
,![]() ,
,
而点![]() ,
,
∴![]() ;
;
①当![]() 是斜边时,如图2,
是斜边时,如图2,
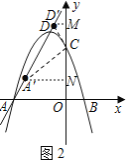
分别过点![]() 、
、![]() 作y轴的垂线交于点N、M,则
作y轴的垂线交于点N、M,则![]() ,
,
则![]() ,即
,即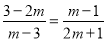 ,
,
解得:![]() (舍去)或
(舍去)或![]() ;
;
②当![]() 是斜边时,如图3,
是斜边时,如图3,
过点![]() 作x轴的平行线交y轴于点N,交过点
作x轴的平行线交y轴于点N,交过点![]() 作y轴的平行线于点M,
作y轴的平行线于点M,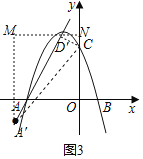
同理可得:![]() ,则
,则![]() ,
,
即![]() ,解得:
,解得:![]() ;
;
③当![]() 是斜边时,
是斜边时,
同理可得:![]() ,解得:
,解得:![]() ,
,
故![]() 或1或 1
或1或 1
则![]() =
=![]() 或
或![]() 或3.
或3.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
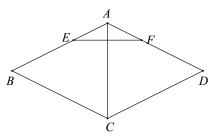
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,已知AB>BC.
(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初三进入中考复习阶段以来,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:A代表睡眠时间4小时,B代表睡眠时间5小时,C代表睡眠时间6小时,D代表睡眠时间7小时,E代表睡眠时间8小时及以上,其中扇形统计图中“E”的圆心角为72°,请你结合统计图所给信息解答下列问题:
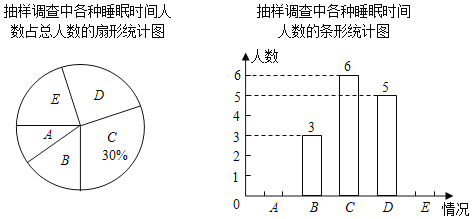
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,井将条形统计图补充完整;
(2)如果把睡眠时间低于7小时称为严重睡眠不足,请估算全校600个初三同学中睡眠严重不足的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
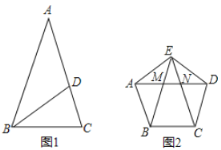
【题目】(1)如图1,已知△ABC中AB=AC,∠BAC=36°,BD是角平分线,求证:点D是线段AC的黄金分割点;
(2)如图2,正五边形的边长为2,连结对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,求MN的长;
(3)设⊙O的半径为r,直接写出它的内接正十边形的长=_________________(用r的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
(1)如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EF GH;(填“>”“=”或“<”)
(2)如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证:![]() =
=![]() ;
;
(3)如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com