
【题目】已知⊙O的半径为2,AB是⊙O的弦,点P在⊙O上,AB=2![]() .若点P到直线AB的距离为1,则∠PAB的度数为_____.
.若点P到直线AB的距离为1,则∠PAB的度数为_____.
【答案】15°或30°或105°
【解析】
如图作OP1⊥AB交⊙O于P1交AB于H,过点O作直线P2P3∥AB交⊙O于P2,P3.首先证明P1,P2,P2是满足条件的点,分别求解即可解决问题.
如图作OP1⊥AB交⊙O于P1交AB于H,过点O作直线P2P3∥AB交⊙O于P2,P3.

∵OA=OB,OH⊥AB,AB=2![]() ,OA=2,
,OA=2,
∴AH=BH=![]() ,
,
∴OH=![]() =1,
=1,
∴HP1=1,
∴直线AB与直线P2P3之间的结论距离为1,
∴P1,P2,P3是满足条件的点.
∵OA=2OH,
∴∠OAH=30°,可得∠BOP1=60°,
∠BOP3=∠AOP2=30°,∠OAP2=∠OP2A=75°,
∴∠P1AB=![]() ∠BOP1=30°,∠P3AB=
∠BOP1=30°,∠P3AB=![]() ∠BOP3=15°,
∠BOP3=15°,
∠P2AB=180°﹣75°=105°.
故答案为:15°或30°或105°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
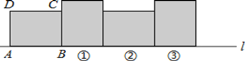
A.288πB.294πC.300πD.396π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是【 】
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;
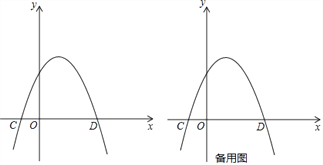
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
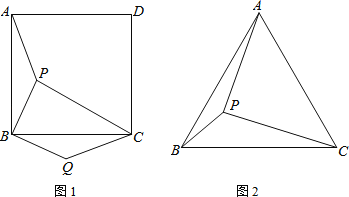
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
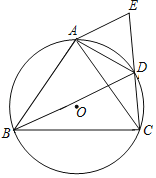
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD内接于⊙O,AB=AC,过点A作AE∥BD交CD的延长线于点E.
(1)求证:AE=DE;
(2)若∠BCD﹣∠CBD=60°,求∠ABD的度数;
(3)在(2)的条件下,若BD=21,CD=9,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
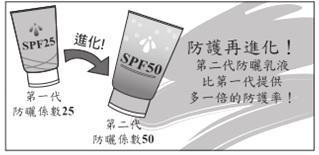
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com