
【题目】如图所示,等边![]() .
.
(1)如图(1),若![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,沿三角形的边顺时针运动,已知点
同时出发,沿三角形的边顺时针运动,已知点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .当点
.当点![]() 第一次到达
第一次到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动.点
同时停止运动.点![]() ,
,![]() 运动______秒后,
运动______秒后,![]() 为等腰三角形.
为等腰三角形.

(2)如图,点![]() 位于等边
位于等边![]() 的内部,且
的内部,且![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①依题意,补全图形;
②若![]() ,
,![]() ,求
,求![]() 与
与![]() 的面积比.
的面积比.

【答案】(1)4秒,16秒;(2)①见解析;②1:4.
【解析】
(1)△AMN是以MN为底边等腰三角形时,证明△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB的长,列出方程,解方程得到答案;
(2)①利用射线的作法得出D点位置,并连接AD,CD;
②证明△CDP是等边三角形,求出AD,CD的长,作CM⊥BD于M,AN⊥BD于N,运用勾股定理求出CM,AN的长,再根据三角形面积公式求出面积比即可.
(1)设点M、N运动t秒后,可得到等边三角形△AMN,如图1,

AM=t,AN=AB-BN=12-2t,
∵△AMN是等边三角形,
∴AM=AN,即t=12-2t,
解得,t=4,
∴点M、N运动4秒后,可得到等边三角形AMN;
当点M、N在BC边上运动时,可以得到以MN为底的等腰三角形,如图2:

∵△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B=60°,
在△ACM和△ABN中,
 ,
,
∴△ACM≌△ABN(AAS)
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y-12,NB=36-2y,
由题意得,y-12=36-2y,
解得:y=16.
若点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,M、N运动的时间为16秒.
(2)①如图所示,

②∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠PCA+∠PCB=60°,
∵∠PCA=∠CBP,
∴∠PCB+∠PBC=60°,
∴∠BPC=180°-60°=120°,
∵∠CPD=180°-∠BPC=60°,PD=PC,
∴△CDP是等边三角形,
∴CD=CP=PD=3,∠DCP=∠ACB=60°,
∴∠DCA=∠PCB,且CA=CB,
∴△DCA≌△PCB(SAS),
∴AD=PB,
∵![]()
∴AD=PB=12,
如图,作CM⊥BD于M,AN⊥BD于N.

∵∠CDP=∠ADP=60°,
∴DM=![]() PD=
PD=![]()
∴CM=![]() ,
,
由△DCA≌△PCB得∠ADC=∠BPC=120°,
∴∠ADP=60°,
∴DN=![]() ,
,
∴AN=![]()
∴


科目:初中数学 来源: 题型:
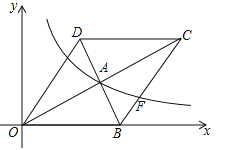
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,新能源汽车以其舒适环保、节能经济的优势受到热捧,随之而来的就是新能汽车销量的急速增加,当前市场上新能漂汽车从动力上分纯电动和混合动力两种,从用途上又分为乘用式和商用式两种,据中国汽车工业协会提供的信息,2017年全年新能源乘用车的累计销量为57.9万辆,其中,纯电动乘用车销量为46.8万辆,混合动力乘用车销量为11.1万辆; 2017年全年新能源商用车的累计销量为19.8万辆,其中,纯电动商用车销量为18.4万辆,混合动力商用车销量为1.4万辆,请根据以上材料解答下列问题:
(1)请用统计表表示我国2017年新能源汽车各类车型销量情况;
(2)小颖根据上述信息,计算出2017年我国新能源各类车型总销量为77.7万辆,并绘制了“2017年我国新能源汽车四类车型销量比例”的扇形统计图,如图1,请你将该图补充完整(其中的百分数精确到0.1%);

(3)2017年我国新能源乘用车销量最高的十个城市排名情况如图2,请根据图2中信息写出这些城市新能源乘用车销售情况的特点(写出一条即可);
(4)数据显示,2018年1~3月的新能源乘用车总销量排行榜上位居前四的厂家是比亚迪、北汽、上汽、江准,参加社会实践的大学生小王想对其中两个厂家进行深入调研,他将四个完全相同的乒乓球进行编号(用“1,2,3,4”依次对应上述四个厂家),并将乒乓球放入不透明的袋子中搅匀,从中一次拿出两个乒乓球,根据乒乓球上的编号决定要调研的厂家.求小王恰好调研“比亚迪”和“江淮”这两个厂家的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
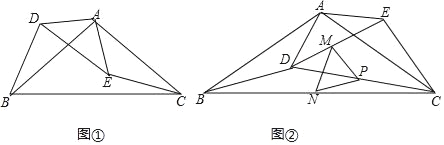
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
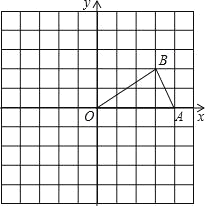
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
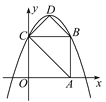
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.

(1)求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积;
(3)拓展提升:如图3,∠E=60°,EC=EB=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com