
【题目】小明从二次函数y=ax2+bx+c的图像(如图)中得出了下面的六条信息:①a<0;②c=0;③函数的最小值为-3;④二次函数y=ax2+bx+c的图像与x轴交于点(0,0),(2.5,0);⑤当0<x1<x2<2时,y1<y2;⑥对称轴是直线x=2.你认为其中正确的是________(填序号).

【答案】②③⑥
【解析】
抛物线开口向上,可判断①;抛物线过原点,可判断②;由图像可知函数最小值,可判断③;由抛物线对称轴以及其与x轴的一个交点可求解抛物线与x轴的另一个交点,可判断④;当x<2时,函数值随x的增大而减小,可判断⑤;由图像可知对称轴,可判断⑥.
解:抛物线开口向上,a>0,故①错误;抛物线过原点,则c=0,故②正确;由图像可知函数最小值为-3,故③正确;抛物线对称轴为x=2,其与x轴的一个交点为(0,0),则可求出抛物线与x轴的另一个交点为(4,0),故④错误;当x<2时,函数值随x的增大而减小,当0<x1<x2<2时,y1>y2,故⑤错误;由图像可知对称轴为x=2,故⑥正确.
故其中正确的是:②③⑥.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,平面直角坐标系中,抛物线
,平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
![]() 该抛物线的解析式;
该抛物线的解析式;
![]() 如图
如图![]() ,点
,点![]() 是所求抛物线上的一个动点,过点
是所求抛物线上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,过点
时,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,则
,则![]() 为何值时,
为何值时,![]() 的面积取得最大值,并求出这个最大.
的面积取得最大值,并求出这个最大.
![]() 如图
如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,![]() ,直角边
,直角边![]() 在
在![]() 轴上,且
轴上,且![]() 与
与![]() 重合,当
重合,当![]() 沿
沿![]() 轴从右向左以每秒
轴从右向左以每秒![]() 个单位长度的速度移动时,设
个单位长度的速度移动时,设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求当
,求当![]() 时,
时,![]() 移动的时间
移动的时间![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于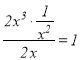 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于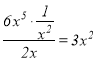 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于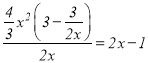 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于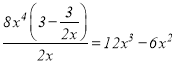 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: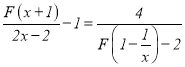 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队同时参与一项工程建设,共同施工15天完成该项工程的![]() ,乙队另有任务调走,甲队又单独施工30天完成了剩余的工程.
,乙队另有任务调走,甲队又单独施工30天完成了剩余的工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若乙队参与该项工程施工的时间不超过13天,则甲队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x﹣2分别交x、y轴于C、A,物线y=﹣
x﹣2分别交x、y轴于C、A,物线y=﹣![]() x2+
x2+![]() x﹣2经过A、C两点,交x轴于另外一点B.点E为线段AC上一点,点F为线段AC延长线一点,AE=CF,点P为AC上方抛物线上的一点,当△PEF是以EF为底边的等腰三角形,且tan∠PFE=
x﹣2经过A、C两点,交x轴于另外一点B.点E为线段AC上一点,点F为线段AC延长线一点,AE=CF,点P为AC上方抛物线上的一点,当△PEF是以EF为底边的等腰三角形,且tan∠PFE=![]() 时,求点P的坐标.
时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
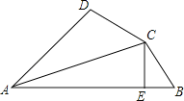
【题目】如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com