
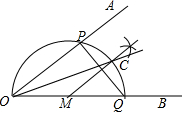
 已知∠AOB,作图.
已知∠AOB,作图.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由OQ为直径可得出OA⊥PQ,结合MC⊥PQ可得出OA∥MC,结论②正确;根据平行线的性质可得出∠POQ=∠CMQ,结合圆周角定理可得出∠COQ=$\frac{1}{2}$∠POQ=∠POC,进而可得出$\widehat{PC}$=$\widehat{CQ}$,OC平分∠AOB,结论①④正确;由∠AOB的度数未知,不能得出OP=PQ,即结论③错误.综上即可得出结论.
解答 解:∵OQ为直径,
∴∠OPQ=90°,OA⊥PQ.
∵MC⊥PQ,
∴OA∥MC,结论②正确;
∵OA∥MC,
∴∠POQ=∠CMQ.
∵∠CMQ=2∠COQ,
∴∠COQ=$\frac{1}{2}$∠POQ=∠POC,
∴$\widehat{PC}$=$\widehat{CQ}$,OC平分∠AOB,结论①④正确;
∵∠AOB的度数未知,∠POQ和∠PQO互余,
∴∠POQ不一定等于∠PQO,
∴OP不一定等于PQ,结论③错误.
综上所述:正确的结论有①②④.
故选C.
点评 本题考查了作图中的复杂作图、角平分线的定义、圆周角定理以及平行线的判定及性质,根据作图的过程逐一分析四条结论的正误是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
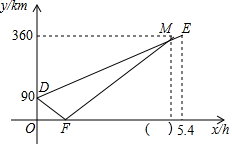 A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
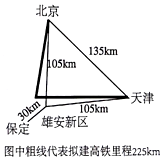 “雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?
“雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com