
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上的两点,
上的两点,![]() 平分
平分![]() ,
,![]() 于
于![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线;
的切线;
![]() 过点
过点![]() 作
作![]() 于
于![]() ,如图
,如图![]() ,判断
,判断![]() 和
和![]() ,
,![]() 之间的数量关系,并证明之;
之间的数量关系,并证明之;
![]() 若
若![]() ,
,![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OC,如图1,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,则有AD⊥CD可判断OC⊥CD,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结CE,如图2,根据角平分线的性质得CD=CF,再证明Rt△ACD≌△ACF得到AD=AF,接着证明Rt△DEC∽Rt△DCA,由相似的性质得DE:DC=DC:DA,然后利用等线段代换即可得到CF2=DEAF;
(3)设⊙O的半径为r,由AD=AF,AD﹣OA=1.5可得到OF=1.5,再证明Rt△ACF∽Rt△ABC,利用相似比可计算出r=3,接着在Rt△FCO中,利用余弦的定义可求出∠COB=60°,然后根据扇形的面积公式和等边三角形面积公式和S阴影部分=S扇形BOC﹣S△BOC进行计算即可.
(1)连接OC,如图1.
∵AC平分∠EAB,∴∠1=∠2.
∵OA=OC,∴∠2=∠3,∴∠1=∠3,∴OC∥AD.
∵AD⊥CD,∴OC⊥CD,∴CD为⊙O的切线;
(2)CF2=AFDE.理由如下:
连结CE,如图2.
∵AC平分∠EAB,CD⊥AE,CF⊥AB,∴CD=CF.在Rt△ACD和△ACF中,![]() ,∴Rt△ACD≌△ACF,∴AD=AF.
,∴Rt△ACD≌△ACF,∴AD=AF.
∵四边形CEAB内接于⊙O,∴∠DEC=∠B.
∵AB是⊙O的直径,∴∠ACB=90°,∴∠ABC+∠2=90°,而∠1+∠ACD=90°,∠1=∠2,∴∠DEC=∠ACD,∴Rt△DEC∽Rt△DCA,∴DE:DC=DC:DA,∴DC2=DEDA,∴CF2=DEAF;
(3)设⊙O的半径为r.
∵AD=AF,而AD﹣OA=1.5,∴AF=AD=OA+OF=r+1.5,∴OF=1.5.
∵∠CAB=∠FAC,∴Rt△ACF∽Rt△ABC,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:r=3或r=﹣
,解得:r=3或r=﹣![]() (舍去).
(舍去).
在Rt△FCO中,∵cos∠COF=![]() =
=![]() =
=![]() ,∴∠COB=60°,∴S阴影部分=S扇形BOC﹣S△BOC
,∴∠COB=60°,∴S阴影部分=S扇形BOC﹣S△BOC
=![]() ﹣
﹣![]() ×32=
×32=![]() π﹣
π﹣![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:
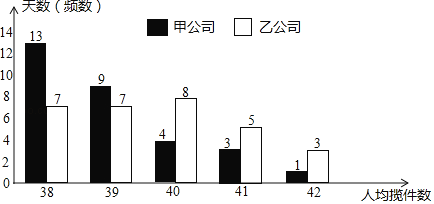
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年圣诞节前夕,小明、小丽两位同学到某超市调研一种袜子的销售情况,
这种袜子的进价为每双 1 元,请根据小丽提供的信息解决小明提出的问题.
小丽:每双定价 2 元,每天能卖出 500 双,而且这种袜子的售价每上涨 0.1 元,其每天的销售量将减少 10 双.
小明:照你所说,如果要实现每天 800 元的销售利润,那该如何定价?别忘了,物价局有规定,售价不能超过进价的 300%呦.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型 | B型 | |
价格(万元/辆) | a | b |
年均载客量(万人/年/辆) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4)

(1)平移线段AB到线段CD,使点A与点C重合,写出点D的坐标.
(2)直接写出线段AB平移至线段CD处所扫过的面积.
(3)平移线段AB,使其两端点都在坐标轴上,则点A的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发在线段BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
⑴如图,求证:△ACE≌△ABD;
⑵求证:BD2+CD2=2AD2;
⑶若AB=4,试问:△DCE的面积有没有最大值,如没有请说明理由,如有请求出最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的爸爸在池边开了一块四边形土地种蔬菜,爸爸让小明计算一下土地的面积,以便计算产量.小明找了米尺和测角仪,测得AB=3米,BC=4米,CD=12米,DA=13米,∠B=90°.
⑴若连接AC,试证明:△ACD是直角三角形;
⑵请你帮小明计算这块土地的面积为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com