
 已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?
已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?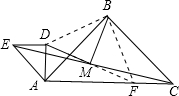
|
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 2014年7月18日下午至19日早晨,超强台风“威马逊”先后在中国海南、广东、广西三省区三次登陆,并造成多人伤亡,多地遭受重创.武警某部队接到救灾命令后火速携带救灾物资乘车赶往省道AB两侧的村庄M、N.已知汽车在直线形的公路AB上由A向B行驶,由于道路泥泞,汽车无法直接到达村庄,需把物资卸在道路上,请你分析:救灾物资应分别卸在什么地方,才能使两村的群众各自在最近的距离拿到救灾物资.请在图上标出这两个位置,并说明理由.
2014年7月18日下午至19日早晨,超强台风“威马逊”先后在中国海南、广东、广西三省区三次登陆,并造成多人伤亡,多地遭受重创.武警某部队接到救灾命令后火速携带救灾物资乘车赶往省道AB两侧的村庄M、N.已知汽车在直线形的公路AB上由A向B行驶,由于道路泥泞,汽车无法直接到达村庄,需把物资卸在道路上,请你分析:救灾物资应分别卸在什么地方,才能使两村的群众各自在最近的距离拿到救灾物资.请在图上标出这两个位置,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
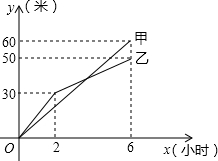 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,请根据图象判断下列信息正确的有( )
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,请根据图象判断下列信息正确的有( )| 1 |
| 10 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com