
【题目】如图,在平面直角坐标系中,函数![]() 的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
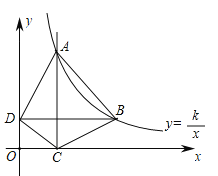
(1)求k的值
(2)若△ABD的面积为4;
①求点B的坐标,
②在平面内存在点E,使得以点A、B、C、E为顶点的四边形是平行四边形,直接写出符合条件的所有点E的坐标.
【答案】(1)4;(2)①(3,![]() ),②(3,
),②(3,![]() );(3,
);(3,![]() );(3,-
);(3,-![]() )
)
【解析】
(1)由点A的坐标,利用反比例函数图象上点的坐标特征可求出k值;
(2)①设AC,BD交于点M,利用反比例函数图象上点的坐标特征可得出点B的坐标,结合AC⊥x轴,BD⊥y轴可得出BD,AM的长,利用三角形的面积公式结合△ABD的面积为4可求出a的值,进而可得出点B的坐标;
②设点E的坐标为(m,n),分AB为对角线、AC为对角线以及BC为对角线三种情况考虑,利用平行四边形的性质(对角线互相平分)可得出关于m,n的二元一次方程组,解之即可得出点E的坐标.
解:(1)∵函数y=![]() (x>0)的图象经过点A(1,4),
(x>0)的图象经过点A(1,4),
∴k=1×4=4.
(2)①设AC,BD交于点M,如图1所示.
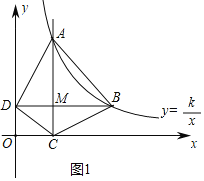
∵点B的横坐标为a(a>1),点B在y=![]() 的图象上,
的图象上,
∴点B的坐标为(a,![]() ).
).
∵AC⊥x轴,BD⊥y轴,
∴BD=a,AM=AC-CM=4-![]() .
.
∵△ABD的面积为4,
∴![]() BDAM=4,即a(4-
BDAM=4,即a(4-![]() )=8,
)=8,
∴a=3,
∴点B的坐标为(3,![]() )
)
②存在,设点E的坐标为(m,n).
分三种情况考虑,如图2所示.
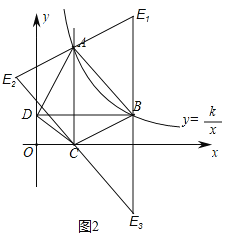
(i)当AB为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴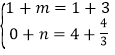 ,解得:
,解得: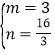 ,
,
∴点E1的坐标为(3,![]() );
);
(ii)当AC为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴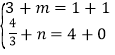 ,解得:
,解得: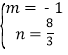 ,
,
∴点E2的坐标为(3,![]() );
);
(iii)当BC为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴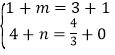 ,解得:
,解得: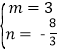 ,
,
∴点E2的坐标为(3,-![]() ).
).
综上所述:点E的坐标为(3,![]() );(3,
);(3,![]() );(3,-
);(3,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,E为边BC上一点,且EC=AD,连接AC.
,E为边BC上一点,且EC=AD,连接AC.
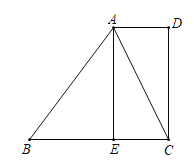
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
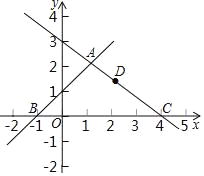
【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展低碳出行”号召,某自行车厂决定生产一批共享单车投入市场.该厂原计划一周生产1400辆共享单车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

⑴根据记录可知前三天共生产 辆;
⑵产量最多的一天比产量最少的一天多生产 辆;
⑶该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=BC,∠BAC的平分线AD交BC于点D,分别过点A作AE∥BC,过点B作BE∥AD,AE与BE相交于点E.若CD=2,则四边形ADBE的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点的初始位置位于数轴上表示
点的初始位置位于数轴上表示![]() 的点,现对
的点,现对![]() 点做如下移动:第
点做如下移动:第![]() 次向左移动
次向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向左移动
点向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,…,依此类推。这样第_____次移动到的点到原点的距离为
点,…,依此类推。这样第_____次移动到的点到原点的距离为![]() .
.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com