
【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
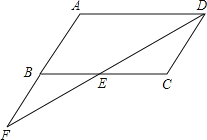
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
【答案】(1)见解析(2)6
【解析】
试题分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE;
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠CDE=∠F,
又∵BF=AB,
∴DC=FB,
在△DCE和△FBE中,
∵
∴△DCE≌△FBE(AAS)
(2)解:∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B100的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在形如ab=N的式子中,我们已经研究两种情况:①已知a和b,求N,这是乘方运算,②已知b和N,求a,这是开放运算,现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算.
定义:如果ab=N,(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:b=logaN,例如求log28,因为23=8,所以
log8=3,又比如∵2﹣3=![]() ,∴log2
,∴log2![]() =﹣3
=﹣3
(1)根据定义计算:
①log381= ②log10=1③如果logx16=4,那么x=
(2)设ax=M,ay=N,则logaM=x,logaN=y(a>0,a≠1,M、N均为正数),
∵ax.ay=ax+y=M.N
∴logaMN=x+y,即logaMN=logaM+logaN
这是对数运算的重要性质之一,进一步,我们还可以得出:
logaM1M2M3…Mn= (其中M1、M2、M3…、Mn均为正数a>0,a≠1)
(3)请你猜想:loga![]() = (a>0,a≠1,M、N均为正数)
= (a>0,a≠1,M、N均为正数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人骑自行车绕800米圆形跑道行驶,他们从同一地点出发,如果方向相反,每一分二十秒相遇一次,如果方向相同,每十三分二十秒相遇一次.假设二人速度不等,求各人速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
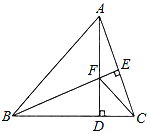
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A(3,2)向左平移4个单位长度得点A′,则点A′关于y轴对称的点的坐标是( )
A.(﹣3,2) B.(﹣1,2) C.(1,﹣2) D.(1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com