
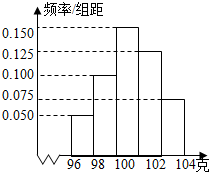
 如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A. | 90 | B. | 108 | C. | 60 | D. | 45 |
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 11+[(-13)+7]=17 | B. | (-2.5)+[5+(-2.5)]=5 | C. | [3$\frac{1}{2}$+(-3$\frac{1}{2}$)]+(-2)=-2 | D. | 3.14+[(-4)+3.14]=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某菜农搭建一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,得抛物线的表达式y=-$\frac{1}{2}{x}^{2}$+2.
某菜农搭建一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,得抛物线的表达式y=-$\frac{1}{2}{x}^{2}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5cm,9cm | B. | 6cm,8cm | C. | 4cm,10cm | D. | 7cm,7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
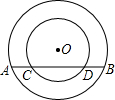 如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )
如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )| A. | 3:2 | B. | $\sqrt{5}$:2 | C. | $\sqrt{5}$:$\sqrt{2}$ | D. | 5:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
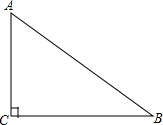 如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.
如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | 6 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com