
| 5 |
| 2 |
| OG2 |
| OF |
| OG2 |
| OF |
| 5 |
| 2 |
|
|
| 5x |
| 3 |
| 5x |
| 3 |
| CG |
| BC |
| CM |
| BO |
| CM |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| OG2 |
| OF |
| DN |
| NE |
| GN |
| DN |
| OG2 |
| OF |
| GN |
| NE |
| OG2 |
| OF |


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:第3章《圆》中考题集(38):3.5 直线和圆的位置关系(解析版) 题型:解答题
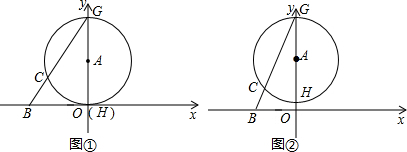
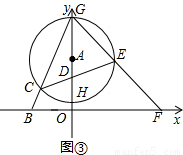
 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.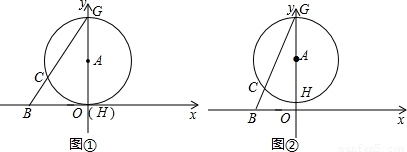
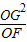 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.查看答案和解析>>
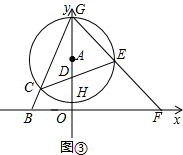
科目:初中数学 来源:第3章《直线与圆、圆与圆的位置关系》中考题集(09):3.1 直线与圆的位置关系(解析版) 题型:解答题
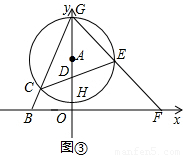
 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.

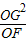 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.查看答案和解析>>
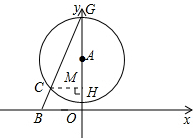
科目:初中数学 来源:第27章《相似》中考题集(15):27.2 相似三角形(解析版) 题型:解答题
 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.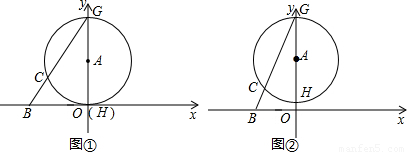
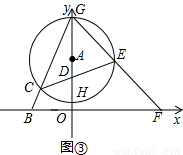
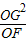 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.查看答案和解析>>
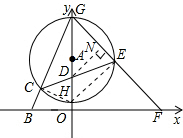
科目:初中数学 来源:第3章《圆》中考题集(37):3.5 直线和圆的位置关系(解析版) 题型:解答题
 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.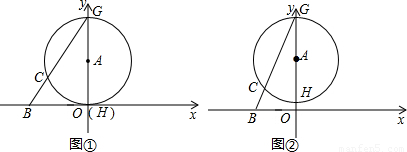
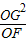 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com