
| A. | $\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}$=$\frac{a}{b}$ | B. | $\frac{(a-b)^{2}}{b-a}$=a-b | ||
| C. | $\frac{{m}^{2}-2m}{4-{m}^{2}}$=-$\frac{m}{m+2}$ | D. | $\frac{0.2a+b}{0.5a-b}$=$\frac{2a+10b}{5a-10b}$ |
分析 根据约分的步骤找出分子与分母的公分母,再约去即可.
解答 解:A、$\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}=\frac{a}{b}$,不符合题意;
B、$\frac{(a-b)^{2}}{b-a}=b-a$,符合题意;
C、$\frac{{m}^{2}-2m}{4-{m}^{2}}=-\frac{m}{m+2}$,不符合题意;
D、$\frac{0.2a+b}{0.5a-b}=\frac{2a+10b}{5a-10b}$,不符合题意;
故选B
点评 本题考查了约分,用到的知识点是分式的基本性质,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.确定公因式要分为系数、字母、字母的指数来分别确定.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
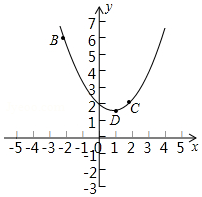 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
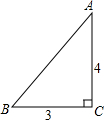 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$.
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
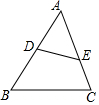 如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.
如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com