
分析 (1)设y=k(x+1.5),再把x=2时,y=7代入求出k的值即可;
(2)设向下平移n个单位经过点(2,-1),再把点(2,-1)代入求出n的值即可.
解答 解:(1)∵y与x+1.5成正比例,
∴设y=k(x+1.5),
∴x=2时,y=7,
∴k(2+1.5)=7,解得k=2,
∴y与x的函数关系式为:y=2x+3,
(2)设向下平移n个单位经过点(2,-1),
∵y与x的函数关系式为y=2x+3,
∴平移后的函数关系式为y=2x+3-n,
∴4+3-n=-1,解得n=8,即下移8个单位.
点评 本题考查的是待定系数法求一次函数的解析式,熟知待定系数法求一次函数解析式的一般步骤是解答此题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
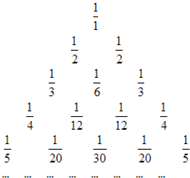 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{p}$=$\frac{q}{n}$ | B. | $\frac{p}{m}$=$\frac{n}{q}$ | C. | $\frac{q}{m}$=$\frac{n}{p}$ | D. | $\frac{m}{n}$=$\frac{p}{q}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
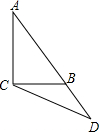 如图,在△ABC中,∠ACB=90°,延长斜边AB到点D,使BD=$\frac{AB}{2}$,连结DC.若tan∠ABC=2,则tan∠BCD的值是$\frac{2}{3}$.
如图,在△ABC中,∠ACB=90°,延长斜边AB到点D,使BD=$\frac{AB}{2}$,连结DC.若tan∠ABC=2,则tan∠BCD的值是$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点.
如图,已知抛物线y=x2-2(m+1)x+m2+1与x轴的相交于A,B两点,与y轴交于C(0,5)点,O为原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com