
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=-![]() x2-
x2-![]() x-3½»xÖįÓŚA”¢BĮ½µć(µćAŌŚµćBµÄ×ó²ą)£¬½»yÖįÓŚµćC.
x-3½»xÖįÓŚA”¢BĮ½µć(µćAŌŚµćBµÄ×ó²ą)£¬½»yÖįÓŚµćC.

(1)ĒóÖ±ĻßACµÄ½āĪöŹ½£»
(2)¢ŁµćPŹĒÖ±ĻßACÉĻ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć(²»ÓėµćA”¢µćCÖŲŗĻ)£¬¹żµćP×÷PD”ĶACÓŚµćD£¬ĒóPDµÄ×ī“óÖµ£»
¢Śµ±Ļ߶ĪPDµÄ³¤¶Č×ī“óŹ±£¬µćQ“ÓµćP³ö·¢£¬ĻČŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹŹµ±µÄĀ·¾¶ŌĖ¶Æµ½yÖįÉĻµÄµćM“¦£¬ŌŁŃŲMCŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æµ½µćCĶ£Ö¹£¬µ±µćQŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠÓĆŹ±×īÉŁŹ±£¬ĒóµćMµÄ×ų±ź£»
øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æµ½µćCĶ£Ö¹£¬µ±µćQŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠÓĆŹ±×īÉŁŹ±£¬ĒóµćMµÄ×ų±ź£»
(3)ČēĶ¼¢Ś£¬½«”÷BOCŃŲÖ±ĻßBCĘ½ŅĘ£¬µćBĘ½ŅĘŗóµÄ¶ŌÓ¦µćĪŖµćB'£¬µćOĘ½ŅĘŗóµÄ¶ŌÓ¦µćĪŖµćO'£¬µćCĘ½ŅĘŗóµÄ¶ŌÓ¦µćĪŖµćC'£¬µćSŹĒ×ų±źĘ½ĆęÄŚŅ»µć£¬ČōŅŌA”¢C”¢O'”¢SĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćO'µÄ×ų±ź.
”¾“š°ø”æ(1)y=-![]() x-3£»(2)¢ŁPD=
x-3£»(2)¢ŁPD=![]() £»¢ŚM(0£¬2)£»(3)Āś×ćĢõ¼žµÄµćO'µÄ×ų±źĪŖ(
£»¢ŚM(0£¬2)£»(3)Āś×ćĢõ¼žµÄµćO'µÄ×ų±źĪŖ(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )»ņ(3£¬-9)»ņ(-
)»ņ(3£¬-9)»ņ(-![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() ).
).
”¾½āĪö”æ
(1)·Ö±šĒó³öÅ×ĪļĻßy=-![]() x2-
x2-![]() x-3ÓėxÖį”¢yÖįµÄ½»µć×ų±ź£¬Č»ŗó·Ö±š°ŃA(-6£¬0)£¬ C(0£¬-3)“śČėÖ±ĻßACµÄ½āĪöŹ½ĪŖy=kx+b ÖŠ£¬½ā¶žŌŖŅ»“Ī·½³Ģ×鼓æÉ.
x-3ÓėxÖį”¢yÖįµÄ½»µć×ų±ź£¬Č»ŗó·Ö±š°ŃA(-6£¬0)£¬ C(0£¬-3)“śČėÖ±ĻßACµÄ½āĪöŹ½ĪŖy=kx+b ÖŠ£¬½ā¶žŌŖŅ»“Ī·½³Ģ×鼓æÉ.
(2)¢ŁÓÉÓŚAC=3![]() ĪŖ¶ØÖµ£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½£¬æÉÖŖµ±”÷PACµÄĆ껿×ī“óŹ±£¬PD×ī“óŹ±£¬ĄūÓĆČż½ĒŠĪµÄĆ껿¹«Ź½Ēó³öµÄ¹ŲĻµŹ½£¬ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹĒó³ö”÷PACµÄĆ껿×ī“óÖµĪŖ
ĪŖ¶ØÖµ£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½£¬æÉÖŖµ±”÷PACµÄĆ껿×ī“óŹ±£¬PD×ī“óŹ±£¬ĄūÓĆČż½ĒŠĪµÄĆ껿¹«Ź½Ēó³öµÄ¹ŲĻµŹ½£¬ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹĒó³ö”÷PACµÄĆ껿×ī“óÖµĪŖ![]() £¬ĄūÓĆS”÷PAC=
£¬ĄūÓĆS”÷PAC=![]() AC”ĮPD£¬¼“æÉĒó³öPDµÄ³¤.
AC”ĮPD£¬¼“æÉĒó³öPDµÄ³¤.
¢ŚĄūÓĆ¹“¹É¶ØĄķæÉĒó³öCN=![]() £¬ĄūÓĆsin”ĻOCN=
£¬ĄūÓĆsin”ĻOCN=![]() £¬æÉĒó³öMK=
£¬æÉĒó³öMK=![]() £¬ “Ó¶ųæɵƵćQŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠµÄŹ±¼äµČÓŚPKµÄ³¤£¬¹żµćP×÷PE”ĶyÖįÓŚµćE£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖÓėyÖį½»µć¼“ĪŖM£¬sin”ĻOCN=sin”ĻEPM=
£¬ “Ó¶ųæɵƵćQŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠµÄŹ±¼äµČÓŚPKµÄ³¤£¬¹żµćP×÷PE”ĶyÖįÓŚµćE£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖÓėyÖį½»µć¼“ĪŖM£¬sin”ĻOCN=sin”ĻEPM=![]() £¬“Ó¶ųĒó³öOM=2£¬¼“µĆMµÄ×ų±ź.
£¬“Ó¶ųĒó³öOM=2£¬¼“µĆMµÄ×ų±ź.
(3)¢ŁČēĶ¼¢Ū”¢Ķ¼¢ÜĄūÓĆĮāŠĪµÄĖÄĢõ±ßĻąµČ£¬æɵĆAC=AO'=3![]() £¬øł¾ŻµćO'ŌŚÖ±Ļßy=-3xÉĻ£¬ÉčO'(m£¬-3m)£¬ĄūÓĆ¹“¹É¶ØĄķ½ØĮ¢µČŹ½£¬½ā³öm¼“æÉ.
£¬øł¾ŻµćO'ŌŚÖ±Ļßy=-3xÉĻ£¬ÉčO'(m£¬-3m)£¬ĄūÓĆ¹“¹É¶ØĄķ½ØĮ¢µČŹ½£¬½ā³öm¼“æÉ.
¢ŚČēĶ¼¢Ż”¢Ķ¼¢Ž£¬Ķ¬¢ŁæɵĆ.
¢ŪČēĶ¼¢ß£¬Ķ¬¢ŁæɵĆ.
(1)½ā£ŗ¶ŌÓŚÅ×ĪļĻßy=-![]() x2-
x2-![]() x-3£¬Įīx=0£¬µĆµ½y=-3£¬
x-3£¬Įīx=0£¬µĆµ½y=-3£¬
”ąC(0£¬-3)£¬
Įīy=0£¬µĆµ½x2+7x+6=0£¬½āµĆx=-6»ņx=-1£¬
”ąA(-6£¬0)£¬B(-1£¬0)£¬
ÉčÖ±ĻßACµÄ½āĪöŹ½ĪŖy=kx+b£¬ŌņÓŠ 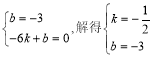 £¬
£¬
”ąÖ±ĻßACµÄ½āĪöŹ½ĪŖy=-![]() x-3.
x-3.
(2)½ā£ŗ¢ŁČēĶ¼¢Ł£¬
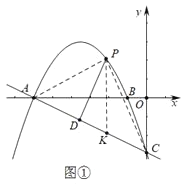
ÉčP(m£¬-![]() m2-
m2-![]() m-3)£¬Į¬½ÓPA”¢PC£¬×÷PK”ĪyÖį½»ACÓŚµćK£¬ŌņK(m£¬-
m-3)£¬Į¬½ÓPA”¢PC£¬×÷PK”ĪyÖį½»ACÓŚµćK£¬ŌņK(m£¬-![]() m-3)£¬
m-3)£¬
”ßPD”ĶAC£¬AC=3![]() ĪŖ¶ØÖµ£¬
ĪŖ¶ØÖµ£¬
”ąPD×ī“óŹ±£¬”÷PACµÄĆ껿×ī“ó£¬
”ßS”÷PAC=![]() ”Į(-
”Į(-![]() m2-3m)”Į6=-
m2-3m)”Į6=-![]() (m+3)2+
(m+3)2+![]() £¬
£¬
”ąm=-3Ź±£¬”÷PACµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ![]() £¬“ĖŹ±P(-3£¬3)£¬
£¬“ĖŹ±P(-3£¬3)£¬![]() ”ĮAC”ĮPD=
”ĮAC”ĮPD=![]() £¬
£¬
”ąPD=![]() .
.
¢ŚČēĶ¼¢Ś£¬
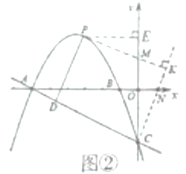
ŌŚxÖįÉĻČ”Ņ»µćN(1£¬0)£¬×÷Ö±ĻßCN£¬¹żµćP×÷PK”ĶCNÓŚµćK£¬½»yÖįÓŚµćM.
”ßOC=3£¬ON=1£¬
”ąCN= ![]() £¬
£¬
”ąsin”ĻOCN=![]() £¬
£¬
”ąMK=![]() £¬
£¬
”ą.µćQŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠµÄŹ±¼ä=![]() =PM+MK=PK£¬
=PM+MK=PK£¬
øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µćM¼“ĪŖĖłĒóµÄµć£¬¹żµćP×÷PE”ĶyÖįÓŚµćE£¬![]() £¬
£¬
”ąEM=1£¬
”ąOM=2£¬
”ąM(0£¬2)
(3)½ā£ŗ¢ŁČēĶ¼¢Ū”¢Ķ¼¢Ü£¬
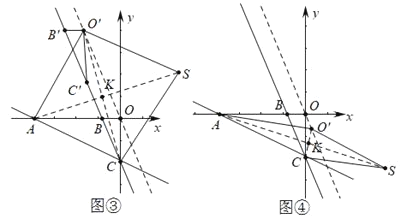
µ±ĖıߊĪACSO'ŹĒĮāŠĪŹ±£¬ÉčAS½»CO'ÓŚµćK£¬AC=AO'=3![]() £¬
£¬
”ßµćO'ŌŚÖ±Ļßy=-3xÉĻ£¬A(-6£¬0)£¬ÉčO'(m£¬-3m)£¬
”ą(m+6)2+(-3m)2=(3![]() )2£¬½āµĆm=
)2£¬½āµĆm= ![]() £¬
£¬
”ąO'(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )£»
)£»
¢ŚČēĶ¼¢Ż”¢Ķ¼¢Ž£¬
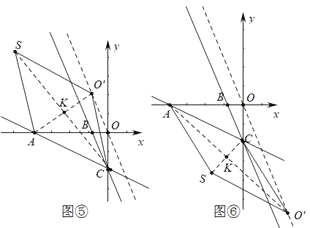
µ±ĖıߊĪACO'SŹĒĮāŠĪŹ±£¬ÉčCS½»AO'ÓŚµćK£¬AC=CO'=3![]() £¬
£¬
”ßµćO'ŌŚÖ±Ļßy=-3xÉĻ£¬C(0£¬-3)£¬ÉčO'(m£¬-3m)£¬
”ąm2+(-3m+3)2=(3![]() )2£¬½āµĆm=3»ņm=-
)2£¬½āµĆm=3»ņm=-![]() £¬
£¬
”ąO'(3£¬-9)»ņ(-![]() £¬
£¬![]() ).
).
¢ŪČēĶ¼¢ß£¬
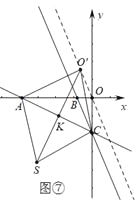
µ±ĖıߊĪASCO'ŹĒĮāŠĪŹ±£¬ÉčAC½»SO'ÓŚµćK£¬AC=3![]() .
.
”ßµćO'ŌŚÖ±Ļßy=-3xÉĻ£¬C(0£¬-3)£¬ÉčO'(m£¬-3m)£¬
”ąm2+(-3m+3)2=(![]() )2+(m+3)2
)2+(m+3)2![]() )£¬½āµĆm=
)£¬½āµĆm=![]() £¬
£¬
”ąO'(![]() £¬
£¬![]() )”£
)ӣ
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄµćO'µÄ×ų±źĪŖ(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )»ņ(3£¬-9)»ņ(-
)»ņ(3£¬-9)»ņ(-![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() ).
).


 ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
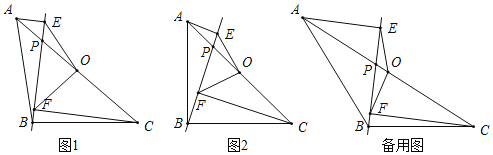
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=BC£¬µćOŹĒACµÄÖŠµć£¬µćPŹĒACÉĻµÄŅ»øö¶Æµć£ØµćP²»ÓėµćA£¬O£¬CÖŲŗĻ£©£®¹żµćA£¬µćC×÷Ö±ĻßBPµÄ“¹Ļߣ¬“¹×ć·Ö±šĪŖµćEŗĶµćF£¬Į¬½ÓOE£¬OF£®
£Ø1£©ČēĶ¼1£¬ĒėÖ±½ÓŠ“³öĻ߶ĪOEÓėOFµÄŹżĮæ¹ŲĻµ£»
£Ø2£©ČēĶ¼2£¬µ±”ĻABC=90”揱£¬ĒėÅŠ¶ĻĻ߶ĪOEÓėOFÖ®¼äµÄŹżĮæ¹ŲĻµŗĶĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ
£Ø3£©Čō|CF©AE|=2£¬EF=2![]() £¬µ±”÷POFĪŖµČŃüČż½ĒŠĪŹ±£¬ĒėÖ±½ÓŠ“³öĻ߶ĪOPµÄ³¤£®
£¬µ±”÷POFĪŖµČŃüČż½ĒŠĪŹ±£¬ĒėÖ±½ÓŠ“³öĻ߶ĪOPµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÕż·½ŠĪABCDµÄ±ß³¤ĪŖ3£¬µćE£¬F·Ö±šŌŚÉäĻßDC£¬DAÉĻŌĖ¶Æ£¬ĒŅDE=DF£®Į¬½ÓBF£¬×÷EH”ĶBFĖłŌŚÖ±ĻßÓŚµćH£¬Į¬½ÓCH£®
£Ø1£©ČēĶ¼1£¬ČōµćEŹĒDCµÄÖŠµć£¬CHÓėABÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ £»
£Ø2£©ČēĶ¼2£¬µ±µćEŌŚDC±ßÉĻĒŅ²»ŹĒDCµÄÖŠµćŹ±£¬£Ø1£©ÖŠµÄ½įĀŪŹĒ·ń³ÉĮ¢£æČō³ÉĮ¢øų³öÖ¤Ć÷£»Čō²»³ÉĮ¢£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼3£¬µ±µćE£¬F·Ö±šŌŚÉäĻßDC£¬DAÉĻŌĖ¶ÆŹ±£¬Į¬½ÓDH£¬¹żµćD×÷Ö±ĻßDHµÄ“¹Ļߣ¬½»Ö±ĻßBFÓŚµćK£¬Į¬½ÓCK£¬ĒėÖ±½ÓŠ“³öĻ߶ĪCK³¤µÄ×ī“óÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
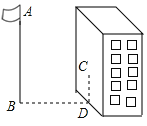
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÄ³Ņ»Ź±æĢ²āµĆ1Ć׳¤µÄÖńøĶŹśÖ±·ÅÖĆŹ±Ó°³¤1.2Ć×£¬ŌŚĶ¬Ņ»Ź±æĢĘģøĖABµÄÓ°³¤²»Č«ĀäŌŚĖ®Ę½µŲĆęÉĻ£¬ÓŠŅ»²æ·ÖĀäŌŚĀ„·æµÄĒ½ÉĻ£¬²āµĆĀäŌŚµŲĆęÉĻµÄÓ°³¤BD=9.6Ć×£¬ĮōŌŚĒ½ÉĻµÄÓ°³¤CD=2Ć×£¬ŌņĘģøĖµÄø߶ČABĪŖ____Ć×.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=kx+bµÄĶ¼ĻóÓė·“±ČĄżŗÆŹży=![]() (x>0)µÄĶ¼Ļó½»ÓŚA(2£¬-1)”¢B(
(x>0)µÄĶ¼Ļó½»ÓŚA(2£¬-1)”¢B(![]() £¬n)Į½µć£¬µćCµÄ×ų±źĪŖ(0£¬2)£¬¹żµćCµÄÖ±ĻßlÓėxÖįĘ½ŠŠ.
£¬n)Į½µć£¬µćCµÄ×ų±źĪŖ(0£¬2)£¬¹żµćCµÄÖ±ĻßlÓėxÖįĘ½ŠŠ.
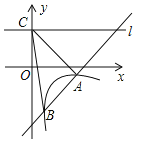
(1)ĒóŅ»“ĪŗÆŹżÓė·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
(2)Ēó”÷ABCµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
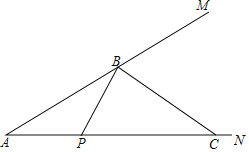
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ĻMAN£½30”ć£¬µćBŌŚ±ßAMÉĻ£¬ĒŅAB£½4![]() £¬µćP“ÓµćA³ö·¢ŃŲÉäĻßAN·½ĻņŌĖ¶Æ£¬ŌŚ±ßANÉĻČ”µćC£ØµćCŌŚµćPÓŅ²ą£©£¬Į¬½įBP£¬BC£®ÉčPC£½m£¬µ±”÷BPC³ÉĪŖµČŃüČż½ĒŠĪµÄøöŹżĒ”ŗĆÓŠ3øöŹ±£¬mµÄÖµĪŖ_____£®
£¬µćP“ÓµćA³ö·¢ŃŲÉäĻßAN·½ĻņŌĖ¶Æ£¬ŌŚ±ßANÉĻČ”µćC£ØµćCŌŚµćPÓŅ²ą£©£¬Į¬½įBP£¬BC£®ÉčPC£½m£¬µ±”÷BPC³ÉĪŖµČŃüČż½ĒŠĪµÄøöŹżĒ”ŗĆÓŠ3øöŹ±£¬mµÄÖµĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µČ±ß”÷AOBµÄ±ß³¤ĪŖ10£¬µćCŌŚ±ßOAÉĻ£¬µćDŌŚ±ßABÉĻ£¬ĒŅOC£½3BD£®·“±ČĄżŗÆŹży£½![]() £Øk”Ł0£©µÄĶ¼ĻóĒ”ŗĆ¾¹żC”¢DĮ½µć£¬ŌņkµÄÖµĪŖ_____£®
£Øk”Ł0£©µÄĶ¼ĻóĒ”ŗĆ¾¹żC”¢DĮ½µć£¬ŌņkµÄÖµĪŖ_____£®
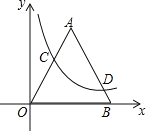
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóG¾¹żµćA£Ø4£¬1£©£¬Ö±Ļßl£ŗy=
£Øx£¾0£©µÄĶ¼ĻóG¾¹żµćA£Ø4£¬1£©£¬Ö±Ļßl£ŗy=![]() +bÓėĶ¼ĻóG½»ÓŚµćB£¬ÓėyÖį½»ÓŚµćC£®
+bÓėĶ¼ĻóG½»ÓŚµćB£¬ÓėyÖį½»ÓŚµćC£®
£Ø1£©ĒókµÄÖµ£»
£Ø2£©ŗį”¢×Ż×ų±ź¶¼ŹĒÕūŹżµÄµć½Š×öÕūµć£®¼ĒĶ¼ĻóGŌŚµćA£¬BÖ®¼äµÄ²æ·ÖÓėĻ߶ĪOA£¬OC£¬BCĪ§³ÉµÄĒųÓņ£Ø²»ŗ¬±ß½ē£©ĪŖw£®
¢Łµ±b=©1Ź±£¬Ö±½ÓŠ“³öĒųÓņWÄŚµÄÕūµćøöŹż£»
¢ŚČōĒųÓņWÄŚĒ”ÓŠ4øöÕūµć£¬½įŗĻŗÆŹżĶ¼Ļó£¬ĒóbµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
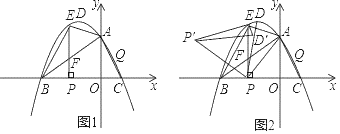
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½©![]() +2ÓėxÖį½»ÓŚB”¢CĮ½µć£¬ÓėyÖį½»ÓŚµćA£¬Å×ĪļĻߵĶ„µćĪŖD£®Į¬½ÓAB£¬µćEŹĒµŚ¶žĻóĻŽÄŚµÄÅ×ĪļĻßÉĻµÄŅ»¶Æµć£¬¹żµćE×÷EP”ĶBCÓŚµćP£¬½»Ļ߶ĪABÓŚµćF£®
+2ÓėxÖį½»ÓŚB”¢CĮ½µć£¬ÓėyÖį½»ÓŚµćA£¬Å×ĪļĻߵĶ„µćĪŖD£®Į¬½ÓAB£¬µćEŹĒµŚ¶žĻóĻŽÄŚµÄÅ×ĪļĻßÉĻµÄŅ»¶Æµć£¬¹żµćE×÷EP”ĶBCÓŚµćP£¬½»Ļ߶ĪABÓŚµćF£®
£Ø1£©Į¬½ÓEA”¢EB£¬Č”Ļ߶ĪACµÄÖŠµćQ£¬µ±”÷EABĆ껿×ī“óŹ±£¬ŌŚxÖįÉĻÕŅŅ»µćRŹ¹µĆ|REŅ»RQ|Öµ×ī“ó£¬ĒėĒó³öRµćµÄ×ų±ź¼°|RE©RQ|µÄ×ī“óÖµ£»
£Ø2£©ČēĶ¼2£¬ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬½«”÷PEDČĘEµćŠż×ŖµĆ”÷ED”äP”䣬µ±”÷AP”äPŹĒŅŌAPĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćP”äµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com