
【题目】在![]() 中,
中,![]() ,
,![]()
![]() ,点D在边
,点D在边![]() 上,将
上,将![]() 绕点A逆时针转,使
绕点A逆时针转,使![]() 与
与![]() 重合,点D的对应点是E.若点B、D、E在同一条直线上,则
重合,点D的对应点是E.若点B、D、E在同一条直线上,则![]() 的度数为_____(用含
的度数为_____(用含![]() 的代数式表示).
的代数式表示).
【答案】90°-1.5![]()
【解析】
由于△ABD绕点A按逆时针方向旋转到△ACE的位置(点B与点C重合,点D与点E重合),根据旋转的性质得到AD=AE,∠BAD=∠CAE,根据等腰三角形的性质得到∠ADE=∠AED,然后根据三角形外角的性质及三角形内角和定理可计算出∠ABD的度数.
∵△ABD绕点A按逆时针方向旋转到△ACE的位置(点B与点C重合,点D与点E重合),∴AD=AE,∠BAD=∠CAE,
∴∠ADE=∠AED.
∵∠BAC=![]() ,
,
∴∠DAE=![]() ,∠ADE=∠AED=∠ABD+∠BAD=∠ABD+
,∠ADE=∠AED=∠ABD+∠BAD=∠ABD+![]() .
.
∵∠DAE+∠ADE+∠AED=180°,
∴![]() +∠ABD+
+∠ABD+![]() +∠ABD+
+∠ABD+![]() =180°,
=180°,
∴∠ABD=![]() =90°-1.5
=90°-1.5![]() .
.
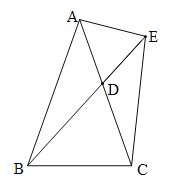
故答案为:90°-1.5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,AB=AD,E是AC的中点.
(1)求证:∠EBD=∠EDB
(2)若∠BED=120°,试判断△BDC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 在平面直角坐标系中的位置如图所示,则下列结论:
在平面直角坐标系中的位置如图所示,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中,正确的结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).

根据以上信息,解答下列问题:
(1)该班共有________名学生.
(2)在条形统计图中,请把空缺部分补充完整.
(3)该班学生所穿校服型号的众数为__________型号,中位数为_________型号.
(4)若该校九年级有学生500人,请你估计穿175型号校服的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣2,1)、B(1,2).

(1)作出点A、B关于x轴的对称点A1、B1,并直接写出A1 、B1 ;
(2)在x轴上找一点P,使PA+PB的值最小,画出点P,并写出点P的坐标;
(3)在如图4×4的正方形网格中,在格点上找一点C,使△ABC为等腰三角形,符合条件的点C的个数为 (直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com