
【题目】若一个三角形的三个顶点均在一个图形的不同的边上,则称此三角形为该图形的内接三角形.
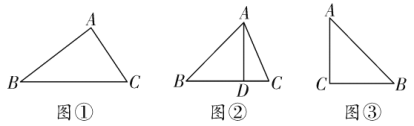
(1)在图①中画出△ABC的一个内接直角三角形;
(2)如图②,已知△ABC中,∠BAC=60°,∠B=45°,AB=8,AD为BC边上的高,探究以D为一个顶点作△ABC的内接三角形,其周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)如图③,△ABC为等腰直角三角形,∠C=90°,AC=6,试探究:△ABC的内接等腰直角三角形的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
【答案】(1)见解析(2)存在,(3)![]()
【解析】
试题分析:(1)根据要求画图即可,体现内接的特点;
(2)如解图②,分别作点D关于AB、AC的轴对称点![]() 、
、![]() ,连接
,连接![]() ,交AB、AC于点E、F,
,交AB、AC于点E、F,
连接DE、DF,则△DEF即为周长最小的内接三角形,然后过点A作AH⊥EF于点H,根据对称性求解即可;
(3)分两种情况讨论:①当内接等腰直角三角形的直角顶点在斜边AB上时;②当内接等腰直角三角形的直角顶点在直角边上时.
试题解析:(1)如解图①,△DEF为所求作的三角形(答案不唯一);
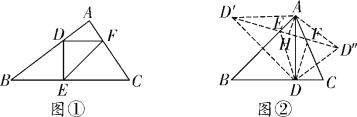
(2)存在.
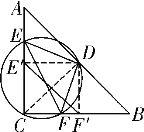
如解图②,分别作点D关于AB、AC的轴对称点![]() 、
、![]() ,连接
,连接![]() ,交AB、AC于点E、F,
,交AB、AC于点E、F,
连接DE、DF,则△DEF即为周长最小的内接三角形,
![]() 的长即为最小周长.
的长即为最小周长.
∵AB=8,∠B=45°,AD⊥BC,∴AD=AB·si45°=![]() .
.
∵点D关于AB、AC的轴对称点分别为![]() 、
、![]() ,
,
∴AD′=![]() =AD=
=AD=![]() ,∠
,∠![]() =2∠BAC=120°,
=2∠BAC=120°,
过点A作AH⊥EF于点H,
在Rt△![]() 中,∠
中,∠![]() =30°,
=30°,
∴![]() =
=![]() ·cos30°=
·cos30°=![]() ,
,
∴△DEF周长的最小值为![]() ;
;
(3)分类讨论:
①当内接等腰直角三角形的直角顶点在斜边AB上时,
如解图③,∵∠ACB=∠EDF=90°,
以EF为直径画圆,则点C、D在圆上,
连接CD,∵DE=DF,
∴∠ACD=∠BCD,又∵AC=BC,
∴CD是AB边上的中线,点D是AB边的中点,
过点D作DE′⊥AC,DF′⊥BC,此时,DE′、DF′最短.
当点E与E′重合,点F与F′重合时,△DEF的面积最小,
此时四边形CEDF为矩形.
设DE=x,则BC=2DE=2x=6,
∴x=3,∴S最小=![]() ;
;
②当内接等腰直角三角形的直角顶点在直角边上时,如解图④,
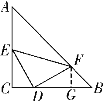
过点F作FG⊥BC于点G,设DG=y,GF=x,易证△CDE≌△GFD,
∴CD=FG=x,
∵∠B=45°,FG⊥BC,
∴GB=GF=x,
∴BC=CD+DG+GB=2x+y=6,即y=6-2x.
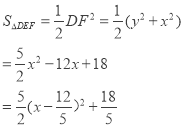
故当x=![]() 时,
时,![]()
∵![]() ,
,
∴△DEF的面积存在最小值,其最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列计算错误的是( )
A.a2÷a0a2=a4B.a2÷(a0a2)=1
C.(a+b)2(a+b)3=a5+b5D.(a+b)(a-b)=a2-b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )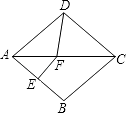
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种长度约为0.000000456毫米的病毒,把0.000000456用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.
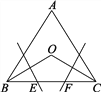
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从车站向东走400米,再向北走500米到小红家;从车站向北走500米,再向西走200米到小强家,则( )
A.小强家在小红家的正东
B.小强家在小红家的正西
C.小强家在小红家的正南
D.小强家在小红家的正北
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com