
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
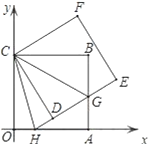
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
【答案】(1)证明见解析;(2)45°;HG= HO+BG;(3)(2,0).
【解析】试题分析:(1)求证全等,观察两个三角形,发现都有直角,而CG为公共边,进而再锁定一条直角边相等即可,因为其为正方形旋转得到,所以边都相等,即结论可证.
(2)上问的结论,本题一般都要使用才能求出结果.所以由三角形全等可以得到对应边、角相等,即BG=DG,∠DCG=∠BCG.同第一问的思路你也容易发现△CDH≌△COH,也有对应边、角相等,即OH=DH,∠OCH=∠DCH.于是∠GCH为![]() 四角的和,四角恰好组成直角,所以∠GCH=90°,且容易得到OH+BG=HG.
四角的和,四角恰好组成直角,所以∠GCH=90°,且容易得到OH+BG=HG.
(3)四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.由上几问知DG=BG,所以此时同时满足DG=AG=EG=BG,即四边形AEBD为矩形.求H点的坐标,可以设其为(x,0),则OH=x,AH=6-x.而BG为AB的一半,所以DG=BG=AG=3.又由(2),HG=x+3,所以Rt△HGA中,三边都可以用含x的表达式表达,那么根据勾股定理可列方程,进而求出x,推得H坐标.
试题解析:(1)∵正方形ABCO绕点C旋转得到正方形CDEF
∴CD=CB,∠CDG=∠CBG=90°
在Rt△CDG和Rt△CBG中
![]()
∴△CDG≌△CBG(HL),
(2)∵△CDG≌△CBG
∴∠DCG=∠BCG,DG=BG
在Rt△CHO和Rt△CHD中
![]()
∴△CHO≌△CHD(HL)
∴∠OCH=∠DCH,OH=DH
∴![]()
HG=HD+DG=HO+BG
(3)四边形AEBD可为矩形
如图,
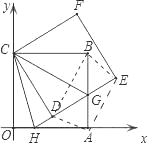
连接BD、DA、AE、EB
因为四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
因为DG=BG,所以此时同时满足DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形.
所以当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形
∴AG=EG=BG=DG
∵AB=6
∴AG=BG=3
设H点的坐标为(x,0)
则HO=x
∵OH=DH,BG=DG
∴HD=x,DG=3
在Rt△HGA中
∵HG=x+3,GA=3,HA=6-x
∴(x+3)2=32+(6-x)2
∴x=2
∴H点的坐标为(2,0).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2![]() ,连接AC.
,连接AC.

(1)求出直线AC的函数解析式;
(2)求过点A,C,D的抛物线的函数解析式;
(3)在抛物线上有一点P(m,n)(n<0),过点P作PM垂直于x轴,垂足为M,连接PC,使以点C,P,M为顶点的三角形与Rt△AOC相似,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.

(1)求证:AM与⊙O相切;
(2)若AM=3DM,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(2)数学测验成绩如下:77,74,65,53,95,87,84,63,91,53,69,81,61,69,91,78,75,81,80,67,76,81,61,69,79,94,86,70,70,87,81,86,90,88,85,67,71,82,87,75,落在79.5~89.5内数据的频数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=2x2向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为( )
A.y=2(x﹣3)2+2
B.y=2(x+3)2+2
C.y=2(x+3)2﹣2
D.y=2(x﹣3)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过 9 秒后边OC与边ON互相垂直.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com