
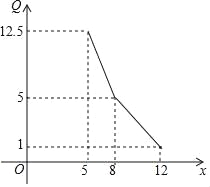
”¾ĢāÄæ”æij×ØĀōµź¾ŹŠ³”µ÷²éµĆÖŖ£¬Ņ»ÖÖÉĢĘ·µÄŌĀĻśŹŪĮæ Q(µ„Ī»£ŗ¶Ö)ÓėĻśŹŪ¼Ūøń x(µ„Ī»£ŗĶņŌŖ/¶Ö)µÄ¹ŲĻµæÉÓĆĻĀĶ¼ÖŠµÄÕŪĻß±ķŹ¾£®
(1)Š“³öŌĀĻśŹŪĮæ Q ¹ŲÓŚĻśŹŪ¼Ūøń x µÄ¹ŲĻµ£»
(2)Čē¹ūøĆÉĢĘ·µÄ½ų¼ŪĪŖ 5 ĶņŌŖ/¶Ö£¬³żČ„½ų»õ³É±¾Ķā£¬×ØĀōµźĻśŹŪøĆÉĢĘ·ĆæŌĀµÄ¹Ģ¶Ø³É±¾ĪŖ 10 ĶņŌŖ£¬ĪŹøĆÉĢĘ· Ćæ¶Ö¶Ø¼Ū¶ąÉŁĶņŌŖŹ±£¬ĻśŹŪøĆÉĢĘ·µÄŌĀĄūČó×ī“ó£æ²¢ĒóŌĀĄūČóµÄ×ī“óÖµ£®
”¾“š°ø”æ£Ø1£©Q=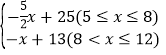 £»£Ø2£©øĆÉĢĘ·Ćæ¶Ö¶Ø¼Ū9ĶņŌŖŹ±£¬ĻśŹŪøĆÉĢĘ·µÄŌĀĄūČó×ī“ó£¬ŌĀĄūČóµÄ×ī“óÖµĪŖ6ĶņŌŖ
£»£Ø2£©øĆÉĢĘ·Ćæ¶Ö¶Ø¼Ū9ĶņŌŖŹ±£¬ĻśŹŪøĆÉĢĘ·µÄŌĀĄūČó×ī“ó£¬ŌĀĄūČóµÄ×ī“óÖµĪŖ6ĶņŌŖ
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·Ø·Ö±šĒó½āæÉµĆ£»
£Ø2£©øł¾ŻŌĀĄūČów=Q£Øx-5£©-10£¬·Ö±š¾Ķ5”Üx”Ü8ŗĶ8£¼x”Ü12Į½ÖÖĒéæöĮŠ³öŗÆŹż½āĪöŹ½£¬Åä·½³É¶„µćŹ½£¬ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹæÉµĆ£®
£Ø1£©µ±5”Üx”Ü8Ź±£¬ÉčQ=ax+b£¬
Ōņ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ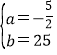 £¬
£¬
”ąQ=-![]() x+25£¬
x+25£¬
Ķ¬ĄķæÉµĆ£¬µ±8£¼x”Ü12Ź±£¬Q=-x+13£¬
ŌņQ= £»
£»
£Ø2£©ŌĀĄūČów=Q£Øx-5£©-10£¬
ÓÉ£Ø1£©ÖŖ£¬w=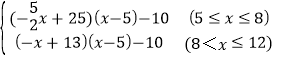 £¬
£¬
¼“w=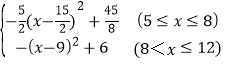 £¬
£¬
ĖłŅŌµ±x=9Ź±£¬wČ”µĆ×ī“óÖµ£¬×ī“óÖµĪŖ6£¬
“š£ŗøĆÉĢĘ·Ćæ¶Ö¶Ø¼Ū9ĶņŌŖŹ±£¬ĻśŹŪøĆÉĢĘ·µÄŌĀĄūČó×ī“ó£¬ŌĀĄūČóµÄ×ī“óÖµĪŖ6ĶņŌŖ£®


 »ĘøŌŠ”דŌŖ½ā¾öĪŹĢāĢģĢģĮ·ĻµĮŠ“š°ø
»ĘøŌŠ”דŌŖ½ā¾öĪŹĢāĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
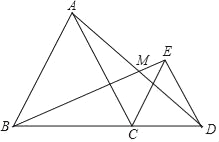
”¾ĢāÄæ”æČēĶ¼£¬B”¢C”¢DŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬”÷ABCŗĶ”÷ECD¶¼ŹĒµČ±ßČż½ĒŠĪ£¬BEÓėADĻą½»ÓŚµćM£¬
£Ø1£©ĒóÖ¤£ŗ”ĻCBE=”ĻCAD£»
£Ø2£©ÓÉ£Ø1£©æÉÖŖ£¬Ķ¼ÖŠµÄ”÷EBCŹĒÓÉ”÷DACŌõŃł±ä»»£ØĢīŅ»Öֱ任£©µĆµ½µÄ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
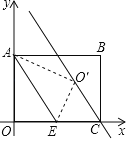
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ¾ŲŠĪOABC£¬µćOĪŖ×ų±źŌµć£¬µćAŌŚyÖįÕż°ėÖįÉĻ£¬µćCŌŚxÖįÕż°ėÖįÉĻ£¬OA£½4£¬OC£½6£¬µćEĪŖOCµÄÖŠµć£¬½«”÷OAEŃŲAE·ÕŪ£¬Ź¹µćOĀäŌŚµćO”䓦£¬×÷Ö±ĻßCO'£¬ŌņÖ±ĻßCO'µÄ½āĪöŹ½ĪŖ£Ø””””£©
A.y£½©x+6B.y£½©![]() x+8C.y£½©
x+8C.y£½©![]() x+10D.y£½©
x+10D.y£½©![]() x+8
x+8
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy=©![]() x2+bx+cÓė×ų±źÖį½»ÓŚA£¬B£¬CČżµć£¬µćAµÄŗį×ų±źĪŖ©1£¬¹żµćC£Ø0£¬3£©µÄÖ±Ļßy=©
x2+bx+cÓė×ų±źÖį½»ÓŚA£¬B£¬CČżµć£¬µćAµÄŗį×ų±źĪŖ©1£¬¹żµćC£Ø0£¬3£©µÄÖ±Ļßy=©![]() x+3ÓėxÖį½»ÓŚµćQ£¬µćPŹĒĻ߶ĪBCÉĻµÄŅ»øö¶Æµć£¬PH”ĶOBÓŚµćH£®ČōPB=5t£¬ĒŅ0£¼t£¼1£®
x+3ÓėxÖį½»ÓŚµćQ£¬µćPŹĒĻ߶ĪBCÉĻµÄŅ»øö¶Æµć£¬PH”ĶOBÓŚµćH£®ČōPB=5t£¬ĒŅ0£¼t£¼1£®
£Ø1£©Č·¶Øb£¬cµÄÖµ£»
£Ø2£©Š“³öµćB£¬Q£¬PµÄ×ų±ź£ØĘäÖŠQ£¬PÓĆŗ¬tµÄŹ½×Ó±ķŹ¾£©£»
£Ø3£©ŅĄµćPµÄ±ä»Æ£¬ŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹”÷PQBĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öĖłÓŠtµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
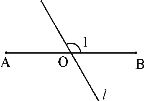
”¾ĢāÄæ”æČēĶ¼£¬AB£½6£¬OŹĒABµÄÖŠµć£¬Ö±Ļßl¾¹żµćO£¬”Ļ1£½120”ć£¬PŹĒÖ±ĻßlÉĻŅ»µć”£µ±”÷APBĪŖÖ±½ĒČż½ĒŠĪŹ±£¬AP£½ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”湓¹É¶ØĄķÉńĆŲ¶ųĆĄĆī£¬ĖüµÄÖ¤·Ø¶ąŃł£¬ĘäÖŠµÄ”°Ć껿·Ø”±øųĮĖĄīĆ÷ĮéøŠ£¬Ėū¾ŖĻ²µŲ·¢ĻÖ£»µ±Į½øöČ«µČµÄÖ±½ĒČż½ĒŠĪČēĶ¼£Ø1£©°Ś·ÅŹ±æÉŅŌĄūÓĆĆ껿·Ø”±Ą“Ö¤Ć÷¹“¹É¶ØĄķ£¬¹ż³ĢČēĻĀ
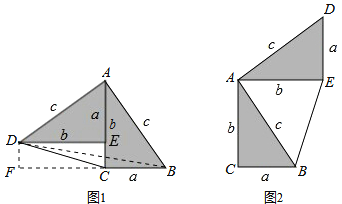
ČēĶ¼£Ø1£©”ĻDAB=90”ć£¬ĒóÖ¤£ŗa2+b2=c2
Ö¤Ć÷£ŗĮ¬½ÓDB£¬¹żµćD×÷DF”ĶBC½»BCµÄŃÓ³¤ĻßÓŚµćF£¬ŌņDF=b-a
SĖıߊĪADCB=![]()
SĖıߊĪADCB=![]()
”ą![]() »Æ¼ņµĆ£ŗa2+b2=c2
»Æ¼ņµĆ£ŗa2+b2=c2
Ēė²ĪÕÕÉĻŹöÖ¤·Ø£¬ĄūÓĆ”°Ć껿·Ø”±Ķź³ÉČēĶ¼£Ø2£©µÄ¹“¹É¶ØĄķµÄÖ¤Ć÷£¬ČēĶ¼£Ø2£©ÖŠ”ĻDAB=90”ć£¬ĒóÖ¤£ŗa2+b2=c2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČ±ßČż½ĒŠĪABCÖŠ£¬DŹĒBC±ßµÄÖŠµć£¬EŹĒABŃÓ³¤ĻßÉĻµÄŅ»µć£¬ĒŅBE=BD£®

£Ø1£©Ēó”ĻBADŗĶ”ĻBDEµÄ¶ČŹż£»
£Ø2£©ĒóÖ¤£ŗAD=DE£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
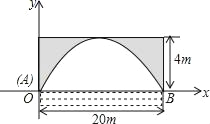
”¾ĢāÄæ”æÓŠŅ»×łÅ×ĪļĻߊĪ¹°ĒÅ£¬Õż³£Ė®Ī»Ź±ĒÅĻĀĖ®ĆęæķĪŖ20m£¬¹°¶„¾ąĖ®Ćę4m£®
£Ø1£©ŌŚČēĶ¼µÄÖ±½Ē×ų±źĻµÖŠ£¬Ēó³öøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ĪŖ±£Ö¤¹żĶł“¬Ö»Ė³Ąūŗ½ŠŠ£¬ĒÅĻĀĖ®Ćęæķ¶Č²»µĆŠ”ÓŚ18m£¬ĒóĖ®ĆęŌŚÕż³£Ė®Ī»»ł“”ÉĻ£¬×ī¶ąÕĒ¶ąÉŁĆ×£¬²»»įÓ°Ļģ¹żĶł“¬Ö»£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”Ļ1£½”Ļ2£¬ŌņĻĀĮŠĢõ¼žÖŠ£¬²»ÄÜŹ¹”÷ABC”Õ”÷DBC³ÉĮ¢µÄŹĒ””£Ø””””£©

A. AB£½CD B. AC£½BD C. ”ĻA£½”ĻD D. ”ĻABC£½”ĻDCB
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com