
【题目】证明:有两边和第三边上的中线对应相等的两个三角形全等。
【答案】见解析.
【解析】
先据题画出图形,写出已知与求证,再分别延长AM到P,使MP=AM,DN到Q,使NQ=DN,连接BP,EQ,用SAS可证△BMP≌△CMA,得∠P=∠CAM,BP=AC,同理可证得∠Q=∠FDN,EQ=DF,于是由SSS可证△ABP≌△DEQ,得∠BAP=∠EDQ,∴∠BAC=∠EDF,再用SAS即可证得结论.
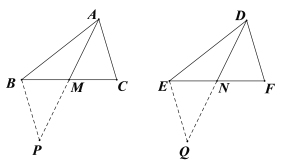
已知:如图,△ABC与△DEF中,AB=DE,AC=DF,BC、EF边上的中线AM=DN.
求证:△ABC≌△DEF.
证明:分别延长AM到P,使MP=AM,DN到Q,使NQ=DN,连接BP,EQ.
∵AM=DN,∴AP=DQ,
∵M是BC的中点,∴BM=CM,
又∵∠BMP=∠CMA,
∴△BMP≌△CMA(SAS),
∴∠P=∠CAM,BP=AC,
同理可证△QEN≌△DFN,
∴∠Q=∠FDN,EQ=DF,
∵AC=DF,∴BP=EQ,
在△ABP和△DEQ中,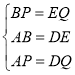 ,
,
∴△ABP≌△DEQ(SSS).
∴∠BAP=∠EDQ,
∴∠BAC=∠EDF,
又AB=DE,AC=DF,
∴△ABC≌△DEF(SAS).
即两边和第三边上的中线对应相等的两个三角形全等.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=–![]() x2+bx+c经过点A(3
x2+bx+c经过点A(3![]() ,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.
,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.
(1)求抛物线的解析式;
(2)连接AB、AC、BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上.
(1)求证:△AED∽△DCG;
(2)若矩形DEFG的面积为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
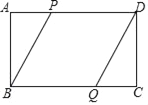
【题目】如图,矩形ABCD中,点P是线段AD上任意一点,点Q为BC上一点,且AP=CQ.
(1)求证:BP=DQ;
(2)若AB=4,且当PD=5时四边形PBQD为菱形.求AD为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
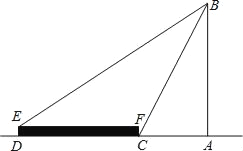
【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com