
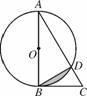
如图5316,在△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
老师给出一个y关于x的函数,甲、乙、丙、丁四位同学各指出这个函数的一个性质:甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:当x<2时,y随x的增大而减小;丁:当x<2时y>0.已知这四位同学叙述都正确。请写出满足上述所有性质的一个函数______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读以下的材料:
如果两个正数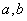 ,即
,即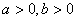 ,有下面的不等式:
,有下面的不等式:
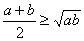 当且仅当
当且仅当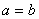 时取到等号
时取到等号
我们把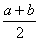 叫做正数
叫做正数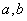 的算术平均数,把
的算术平均数,把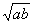 叫做正数
叫做正数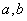 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知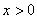 ,求函数
,求函数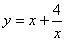 的最小值。
的最小值。
解:令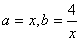 ,则有
,则有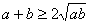 ,得
,得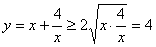 ,当且仅当
,当且仅当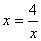 时,即
时,即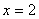 时,函数有最小值,最小值为
时,函数有最小值,最小值为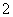 。
。
根据上面回答下列问题
① 已知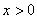 ,则当
,则当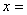 时,函数
时,函数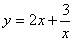 取到最小值,最小值
取到最小值,最小值
为 ;
② 用篱笆围一个面积为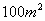 的矩形花园,问这个矩形的长、宽各为多
的矩形花园,问这个矩形的长、宽各为多 少时,所
少时,所
用的篱笆最短,最短的篱 笆周长是多少;
笆周长是多少;
③. 已知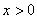 ,则自变量
,则自变量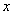 取何值时,函数
取何值时,函数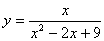 取到最大值,最大值为多少?
取到最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
若⊙O的半径为4 cm,点A到圆心O的距离为3 cm,那么点A与⊙O的位置关系是( )
A.点A在圆内 B.点A在圆上 C.点A在圆外 D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
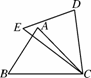
如图4217,在△ABC和△DEC中,已知AB=DE,还需要添加两个条件才能使△ABC≌△DEC,不能添加的一组是( )
A.BC=EC,∠B=∠E B.BC=EC, AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com