练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知x=-1是关于x的方程x2+2ax+a2=0的一个根，求a的值．

    分析 根据一元二次方程解的定义，把x=-1代入x2+2ax+a2=0得到关于a的一元二次方程1-2a+a2=0，然后解此一元二次方程即可．

    解答 解：把x=-1代入x2+2ax+a2=0得1-2a+a2=0，
    解得a1=a2=1，
    所以a的值为1．

    点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

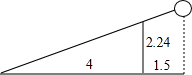    6．已知女排赛场标准球网的高度是2.24米，在2016年奥运会女排比赛中，某队球员在一次扣球时，球恰好擦网而过（击球擦网落地过程为直线），落在对方场地距离球网4米的位置上，此时该运动员距离球网1.5米，则该运动员击球的高度是3.08米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列说法正确的是（　　）
    A．（-3）2的算术平方根是3B．$\sqrt{225}$的平方根是±15
    C．当x=0或2时，x$\sqrt{x-2}$=0D．$\frac{\sqrt{3}}{2}$是分数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴交于A，B两点（点A在点B的左侧，与y轴交于点C，点B的坐标为（4，0），将直线y=kx沿y轴向上平移4个单位长度后恰好经过B，C两点．
    （1）求直线BC及抛物线的解析式；
    （2）将直线BC沿y轴向上平移5个单位长度后与抛物线交于D，E两点，若点P是抛物线位于直线BC下方的一个动点，连接PD，交直线BC于点Q，连接PE和PQ，设△PEQ的面积为S，当S取得最大值时，求出此时点P的坐标及S的最大值．
    （3）如图2，记（2）问中直线DE与y轴交于M点，现有一点N从M点出发，先沿y轴到达K点，再沿KB到达B点，已知N点在y轴上运动的速度是每秒2个单位长度，它在直线KB上运动速度是1个单位长度，现要使N点按照上述要求到达B点所用的时间最短，请简述确定K点位置的过程，求出点K的坐标，不要求证明．

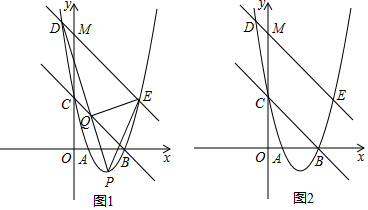
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

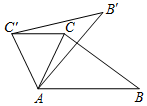    11．如图，在△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A按逆时针方向旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=（　　）
    A．30°B．35°C．40°D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：（-3）2÷2$\frac{1}{4}$-（-$\frac{4}{3}$）×（-$\frac{3}{8}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知x2-4x-5=0，则分式$\frac{6x}{{x}^{2}-x-5}$的值是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列调查中，最适合采用普查方式的是（　　）
    A．调查2017年春节晚会的收视率
    B．调查宝应湖中鱼的种类和数量
    C．调查某品牌节能灯的使用寿命
    D．调查某航班的旅客是否携带了违禁物品

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图1，正方形ABCD的顶点A在原点O处，点B在x轴上，点C的坐标为（6，6），点D在y轴上，动点P，Q各从点A，D同时出发，分别沿AD，DC方向运动，且速度均为每秒1个单位长度．
    （1）探索AQ与BP有什么样的关系？并说明理由；
    （2）如图2，当点P运动到线段AD的中点处时，AQ与BP交于点E，求线段CE的长．
    （3）如图3，设运动t秒后，点P仍在线段AD上，AQ交BD于F，且△BPQ的面积为S，试求S的最小值，及当S取最小值时∠DPF的正切值．

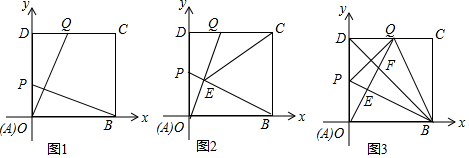
    查看答案和解析>>

    同步练习册答案