
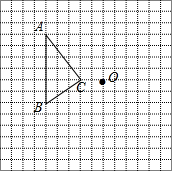
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′.  金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 如果a2=b2,则a=b | |
| B. | 两边一角对应相等的两个三角形全等 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | x=2 y=1是方程2x-y=3的解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,△ABC的三个顶点均在格点上,将△ABC绕点O旋转180°后得到三角A′B′C′,则点B的对应点B′的坐标为( )
如图,在平面直角坐标系中,△ABC的三个顶点均在格点上,将△ABC绕点O旋转180°后得到三角A′B′C′,则点B的对应点B′的坐标为( )| A. | (-2,-1) | B. | (-3,3) | C. | (1,3) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则AE的长度为2$\sqrt{7}$.
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则AE的长度为2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{●=8}\\{★=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{●=-8}\\{★=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{●=-8}\\{★=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{●=8}\\{★=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,给出的是2016年1月份的日历表,任意画出一竖列上相邻的三个数,请你运用方程思想进行研究,则这三个数的和不可能是( )
如图所示,给出的是2016年1月份的日历表,任意画出一竖列上相邻的三个数,请你运用方程思想进行研究,则这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 40 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A.
在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com