
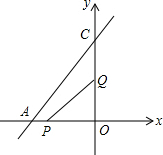
 如图已知直线AC的函数解析式为y=$\frac{4}{3}$x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
如图已知直线AC的函数解析式为y=$\frac{4}{3}$x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位? 分析 根据直线AC的解析式可得出点A、C的坐标,设运动时间为t,则PO=|t-6|,OQ=2t,根据三角形的面积即可得出关于t的一元二次方程,解方程即可得出结论.
解答 解:∵直线AC的函数解析式为y=$\frac{4}{3}$x+8,
∴点C(0,8),点A(-6,0).
设运动时间为t,则PO=|t-6|,OQ=2t,
根据题意,得:2t×|t-6|=16,
解得:t1=2,t2=4,t3=3-$\sqrt{17}$(舍去),t4=3+$\sqrt{17}$.
∴经过2秒、4秒或3+$\sqrt{17}$秒后能使△POQ的面积为8个平方单位
点评 本题考查了一元二次方程的应用,根据三角形的面积找出关于t的一元二次方程是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a,b为有理数,且它们在数轴上的位置如图所示.
已知a,b为有理数,且它们在数轴上的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 模球次数 | 15 | 80 | 180 | 600 | 1000 |
| 模到白球次数 | 5 | 21 | 39 | 250 | |
| 模到白球的频率 | 0.33 | 0.26 | 0.21 | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com