
观察计算:
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
探究证明:
如图所示, 为圆O的内接三角形,
为圆O的内接三角形, 为直径,过C作
为直径,过C作 于D,设
于D,设 ,BD=b.
,BD=b.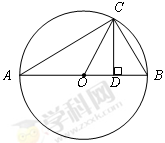
(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出 与
与 的大小关系是:______________.
的大小关系是:______________.
实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
观察计算:当 ,
, 时,
时, >
> ;当
;当 ,
, 时,
时, =
= .
.
探究证明:(1)OC= ,
,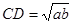 ;
;
(2)当a=b时,OC=CD, =
= ;a≠b时,OC>CD,
;a≠b时,OC>CD, >
> .
.
结论归纳:
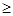
 .
.
实践应用:周长最小为4米.
解析试题分析:观察计算:把 ,
, 和
和 ,
, 分别代入
分别代入 与
与 计算,即可作出判断;
计算,即可作出判断;
探究证明:(1)由于OC是直径AB的一半,则OC易得.通过证明△ACD∽△CBD,可求CD;
(2)分a=b,a≠b讨论可得出 与
与 的大小关系;
的大小关系;
实践应用:通过前面的结论长方形为正方形时,周长最小.
试题解析:观察计算:当 ,
, 时,
时, >
>
当 ,
, 时,
时, =
= .
.
探究证明:
(1)∵AB=AD+BD=2OC,
∴OC=
∵AB为⊙O直径,
∴∠ACB=90°.
∵∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∴△ACD∽△CBD.
∴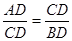 .即CD2=AD•BD=ab,解得
.即CD2=AD•BD=ab,解得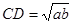 ;
;
(2)当a=b时,OC=CD, =
= ;
;
a≠b时,OC>CD, >
> .
.
结论归纳:
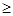
 .
.
实践应用
设长方形一边长为x米,则另一边长为 米,设镜框周长为l米,
米,设镜框周长为l米,
则 ,当
,当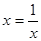 ,即x=1(米)时,镜框周长最小.
,即x=1(米)时,镜框周长最小.
此时四边形为正方形时,周长最小为4米.
考点:1.几何不等式;2.相似三角形的判定与性质;3.圆周角定理


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
已知,如图,在平行四边形ABCD中,E、F分别是边BC、CD上的点,且EF∥BD,AE、AF分别交BD于点G和点H,BD=12,EF=8。求:(1) 的值。(2)线段GH的长。
的值。(2)线段GH的长。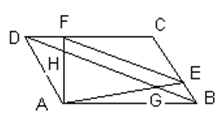
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题: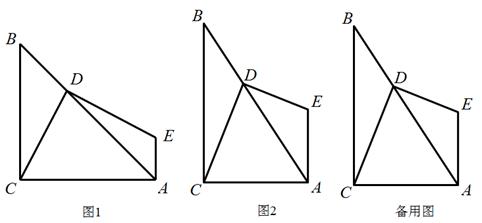
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AB于E.
(1)证明△PAE∽△CDP;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设AP=x,BE=y,求y与x的函数关系式及y的取值范围;
(3)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图:四边形ABCD和四边形AEFC都是矩形,点B在EF边上.
(1)请你找出图中一对相似三角形(相似比不等于1),并加以证明;
(2)若四边形ABCD的面积为20,求四边形AEFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在正方形网格上有△ABC和△DEF.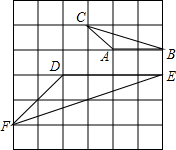
(1)求证:△ABC∽△DEF;
(2)计算这两个三角形的周长比;
(3)根据上面的计算结果,你有何猜想?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com