Question

5．如图，平面直角坐标系内一点P（m，2），过点P作直线PA∥x轴交抛物线y=ax²+1（a≠0）于A，B两点（点A在点B的左侧），其中点A的横坐标为-2，过P作PE⊥x轴交抛物线于点E，连结AE．
（1）求a的值．
（2）当m≥2时，①PE=$\frac{1}{4}$m²-1（用m的代数式表示），
②若PE=2BP，求此时点E的坐标．
（2）过点A作AD⊥AE，且AD=AE，问是否存在m使得点D落在坐标轴上？若存在，请求出m的值？若不存在．请说明理由．

Answer 1

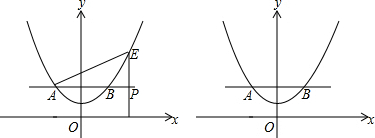
分析 （1）求出点A坐标，代入抛物线解析式即可解决问题．
（2）①求出点E坐标，根据PE=E_y-P_y，即可解决问题．
②根据PE=2BP，列出方程即可解决问题．
（3）三种情形①如图1中，作DF⊥AB于F，由△ADF≌△EAP，推出DF=AP=2，由此即可解决问题．②如图2中，作AF⊥x轴于F，EG⊥FA于G．方法类似①，③如图3中，由△AEP≌△DAG，可得AG=EP=2，即可解决问题．

解答 解：（1）∵PA∥x轴，P（m，2），点A横坐标为-2，
∴点A坐标为（-2，2），代入y=ax²+1，
解得a=$\frac{1}{4}$，

（2）①∵抛物线解析式为y=$\frac{1}{4}$x²+1，
∴B（2，2），
∵m≥2，
∴点E在直线AB上方，E（m，$\frac{1}{4}$m²+1），
∴PE=$\frac{1}{4}$m²+1-2=$\frac{1}{4}$m²-1．
故答案为$\frac{1}{4}$m²-1．

②∵PE=2PB，
∴$\frac{1}{4}$m²-1=2（m-2），
∴m²-8m+12=0，
∴m=2或6．
m=2时，P、E、B三点重合不合题意，舍弃．
∴m=6．

（3）①如图1中，作DF⊥AB于F，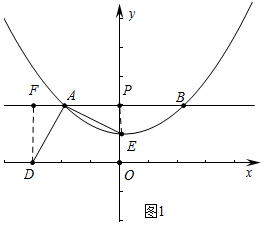

∵DA⊥AE，
∴∠DAE=∠DFA=∠APE=90°，
∵∠DAF+∠EAG=90°，∠DAF+∠ADF=90°，
∴∠ADF=∠EAP，∵AD=AE，
∴△ADF≌△EAP，
∴DF=AP=2，
∵A（2，2），
∴点P在y轴上，点E在y轴上，
∴点E坐标（0，1），
∴m=0，

②如图2中，作AF⊥x轴于F，EG⊥FA于G．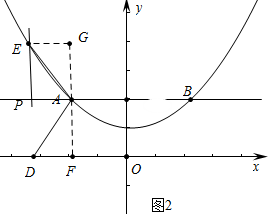

同理可证△AEG≌△DAF，
∴AF=EG=2，
∴E（-4，5）．
∴m=-4．

③如图3中，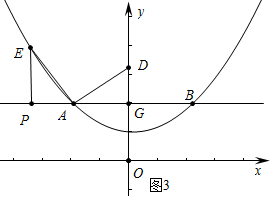

由△AEP≌△DAG，可得AG=EP=2，
∴点E纵坐标为4，
∴4=$\frac{1}{4}$x²+1，
x=±2$\sqrt{3}$，
∴点E坐标为（-2$\sqrt{3}$，4），
∴m=-2$\sqrt{3}$
综上所述，当m=0或-4或-2$\sqrt{3}$时，满足条件的点D在坐标轴上．

点评 本题考查二次函数综合题、一元二次方程、全等三角形的判定和性质等知识，解题的关键是熟练应用这些知识解决问题，学会分类讨论，需要正确画出图形解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．