
 如图,AB是⊙O的直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF.
如图,AB是⊙O的直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF.分析 (1)过点O作OH⊥EF于H,如图,根据切线的性质得AB⊥AC,然后根据角平分线的性质得OH=OA,然后根据切线的判定方法可判断EF为⊙O的切线;
(2)过E点作EG⊥BD于G,如图,根据切线的性质得AB⊥BD,则四边形ABGE为矩形,所以EG=AB,BG=AE=4,再根据切线长定理得到EH=EA=4,FH=FB=9,则GF=BF-BG=5,EF=EH+FH=13,
然后在Rt△EGF中利用勾股定理计算出EG即可得到⊙O的半径.
解答 解:(1)EF与⊙O相切.理由如下:
过点O作OH⊥EF于H,如图,
∵AB是⊙O的直径,AC是⊙O的切线,
∴AB⊥AC,
∵EO平分∠AEF,
而OH⊥EF,
∴OH=OA,
∴EF为⊙O的切线;
(2)过E点作EG⊥BD于G,如图,
∵AB是⊙O的直径,BD是⊙O的切线,
∴AB⊥BD,
∴四边形ABGE为矩形,
∴EG=AB,BG=AE=4,
∵EF为⊙O的切线,
∴EH=EA=4,FH=FB=9,
∴GF=BF-BG=5,EF=EH+FH=13,
在Rt△EGF中,EG=$\sqrt{E{F}^{2}-F{G}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴AB=12,
∴⊙O的半径为6.
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”; 有切线时,常常“遇到切点连圆心得半径”.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
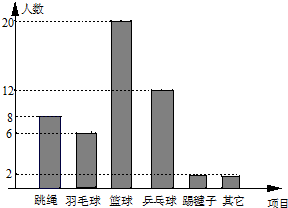 小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )
小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )| A. | 144° | B. | 75° | C. | 180° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com