
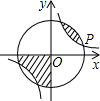
 如图,点P(4a,a)是反比例函数y=$\frac{k}{x}$(k>0)与⊙O的一个交点,图中阴影部分的面积为17π,则反比例函数的解析式为y=$\frac{16}{x}$.
如图,点P(4a,a)是反比例函数y=$\frac{k}{x}$(k>0)与⊙O的一个交点,图中阴影部分的面积为17π,则反比例函数的解析式为y=$\frac{16}{x}$. 分析 根据反比例函数图象的对称性得到圆的面积=4×17π=68π,再计算出圆的半径=2$\sqrt{17}$,然后利用勾股定理得到16a2+a2=(2$\sqrt{17}$)2,解得a=2或-2(舍去),则P点坐标为(8,2),然后根据反比例函数图象上点的坐标特征求得k.
解答 解:∵图中阴影部分的面积为17π,
∴圆的面积=4×17π=68π,
∴圆的半径=2$\sqrt{17}$,
∵P(4a,a)在圆上,
∴16a2+a2=(2$\sqrt{17}$)2,解得a=2或-2(舍去),
∴P点坐标为(8,2),
把P(8,2)代入y=$\frac{k}{x}$得k=8×2=16,
∴反比例函数的解析式为y=$\frac{16}{x}$.
故答案为y=$\frac{16}{x}$.
点评 本题考查了待定系数法以及反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①二、四象限的角平分线y=-x;②一、三象限的角平分线y=x;对称中心是:坐标原点.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
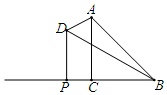 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )| A. | 一直变大 | B. | 一直变小 | C. | 先变小再变大 | D. | 先变大再变小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
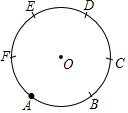 尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )| A. | ② | B. | ①② | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com