
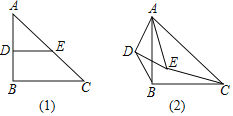
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点D、E分别是边AB、AC的中点,连接DE,将△ADE绕点A按顺时针方向旋转,记旋转角为α,BD、CE所在直线相交所成的锐角为β.
(1)问题发现当α=0°时,![]() =_____;β=_____°.
=_____;β=_____°.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 和β的大小有无变化?请仅就图2的情形给出证明.
和β的大小有无变化?请仅就图2的情形给出证明.
(3)在△ADE旋转过程中,当DE∥AC时,直接写出此时△CBE的面积.
【答案】(1)![]() ,45;(2)
,45;(2)![]() 和β的大小无变化;(3)△BCE的面积为4或12.
和β的大小无变化;(3)△BCE的面积为4或12.
【解析】
(1)利用等腰直角三角形的性质,线段的中点的定义即可判断.
(2)结论:![]() 和β的大小无变化.如图2中,延长CE交AB于点O,交BD于K.证明△DAB∽△EAC,即可解决问题.
和β的大小无变化.如图2中,延长CE交AB于点O,交BD于K.证明△DAB∽△EAC,即可解决问题.
(3)分两种情形:①当点D在线段AB上时,②当点D在线段BA的延长线上时,分别求解即可.
解:(1)如图1中,
∵∠B=90°,BA=BC,
∴∠A=45°,AC=![]() AB,
AB,
∵点D、E分别是边AB、AC的中点,
∴BD=![]() AB,EC=
AB,EC=![]() AC,
AC,
∴![]() =
=![]() ,β=45°,
,β=45°,
故答案为![]() ,45.
,45.
(2)结论:![]() 和β的大小无变化.
和β的大小无变化.
理由:如图2中,延长CE交AB于点O,交BD于K.

∵AE=![]() AD,AC=
AD,AC=![]() AB,
AB,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
∴△DAB∽△EAC,
∴![]() =
=![]() =
=![]() ,∠OBK=∠OCA,
,∠OBK=∠OCA,
∵∠BOK=∠COA,
∠BKO=∠CAO=45°,
∴![]() 和β的大小无变化.
和β的大小无变化.
(3)当点D在线段AB上时,S△BCE=![]() ×4×2=4,
×4×2=4,
当点D在线段BA的延长线上时,S△BCE=![]() ×4×6=12.
×4×6=12.
综上所述,△BCE的面积为4或12.


科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月24日,工信部发布《关于推动![]() 加快发展的通知》,全力推进
加快发展的通知》,全力推进![]() 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向
网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向![]() 迁移,推动“
迁移,推动“![]() 医疗健康”创新发展,实施“
医疗健康”创新发展,实施“![]() 工业互联网”512工程,促进“
工业互联网”512工程,促进“![]() 车联网”协同发展,构建
车联网”协同发展,构建![]() 应用生态系统.现“
应用生态系统.现“![]() 网络”已成为一个热门词汇,某校为了解九年级学生对“
网络”已成为一个热门词汇,某校为了解九年级学生对“![]() 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
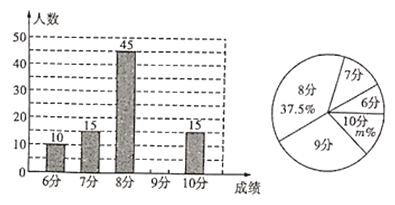
(1)请补全条形统计图,扇形统计图中![]() __;
__;
(2)所调查学生成绩的众数是_ ____分,平均数是_ 分;
(3)若该校九年级学生有![]() 人,请估计得分不少于
人,请估计得分不少于![]() 分的有多少人?
分的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
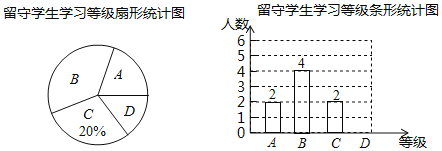
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
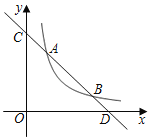
【题目】如图,已知一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求反比例函数和一次函数的解析式;
(2)求y1<y2时,自变量x的取值范围;
(3)若点P是x轴上一动点,当△ABP为直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
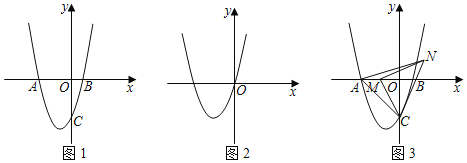
【题目】已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
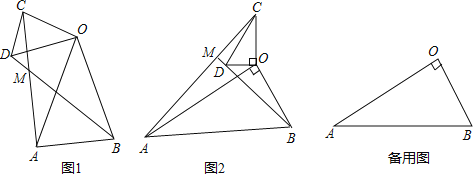
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

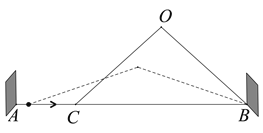
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com