
【题目】如图,在平行四边形ABCD中,![]() 的平行线
的平行线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)请指出图中平行四边形的个数,并说明理由;
(2)![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?

【答案】(1)图中平行四边形有3个:平行四边形ABCD、平行四边形AMQC、平行四边形APNC;(2)MP=QN,理由见解析.
【解析】(1)由已知易得图中有3个平行四边形,分别是平行四边形ABCD、平行四边形AMQC和平行四边形APNC,由已知条件根据平行四边形的判定方法进行分析证明即可;
(2)MP=QN,由(1)可知四边形AMQC和四边形APNC都是平行四边形,由此可得MQ=AC=PN,由此可得MQ-PQ=PN-PQ,从而可得MP=QN.
(1)图中平行四边形有3个:平行四边形ABCD、平行四边形AMQC、平行四边形APNC,理由如下:
①四边形ABCD是平行四边形是已知条件;
②四边形APNC是平行四边形的理由:
∵AC∥MN AB∥CD
∴ ∠MPA=∠PAC ∠MPA=∠N
∴∠PAC=∠N
∵AB∥CD
∴ ∠PAC+∠ACN=180°,∠N+∠APN=180°,
∴∠ACN=∠APN,
∴四边形APNC是平行四边形(两组对角分别相等的四边形是平行四边形)
③四边形AMQC是平行四边形的理由:
∵AC∥MN, AD∥BC,
∴ ∠M=∠DAC ,∠DAC=∠ACQ,
∴∠M=∠ACQ,
∵AC∥MN,
∴ ∠M+∠MAC=180°, ∠MQC+∠ACQ=180°,
∴∠MAC=∠MQC,
∴四边形AMQC是平行四边形(两组对角分别相等的四边形是平行四边形)
(2)MP=QN,理由如下:
∵由(1)可知四边形AMQC和四边形APNC都是平行四边形,
∴MQ=AC=PN,
∴MQ-PQ=PN-PQ,
∴MP=QN.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】一种笔记本的售价为2.2元/本,如果买100本以上,超过100本部分的售价为2元/本.
(1)小强和小明分别买了50本和200本,他们俩分别花了多少钱?
(2)如果小红买这种笔记本花了380元,她买了多少本?
(3)如果小红买这种笔记本花了n元,她又买了多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点. 
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生产小组有![]() 名工人,调查每个工人的日均零件生产能力,获得如表数据:
名工人,调查每个工人的日均零件生产能力,获得如表数据:
日均生产零件的个数(个) |
|
|
|
|
|
|
工人人数(人) |
|
|
|
|
|
|
![]() 求这
求这![]() 名工人日均生产零件的众数、中位数、平均数.
名工人日均生产零件的众数、中位数、平均数.
![]() 为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.
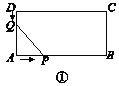
设点P,Q同时出发,用t(s)表示移动的时间.
(发现) DQ=________cm,AP=________cm.(用含t的代数式表示)
(拓展)(1)如图①,当t=________s时,线段AQ与线段AP相等?
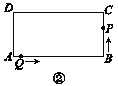
(2)如图②,点P,Q分别到达B,A后继续运动,点P到达点C后都停止运动.
当t为何值时,AQ=![]() CP?
CP?
(探究)若点P,Q分别到达点B,A后继续沿着A—B—C—D—A的方向运动,当点P与点Q第一次相遇时,请直接写出相遇点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律
在数轴上,把表示数1的点称为基准点,记作点O.对于两个不同点M和N,若点M和点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图1中MO=NO=2,则点M和点N互为基准变换点.
发现:(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b= ;若a=4,则b= ;
②用含a的式子表示b,则b= ;
应用:(2)对点A进行如下操作:先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
探究:(3)点P是数轴上任意一点,对应的数为m,对P点做如下操作:P点沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的基准变换点,点P2沿数轴向右移动k个单位长度得到点P3,点P4为P3的基准变换点,“…依次顺序不断的重复,得到P6…,求出数轴上点P2018表示的数是多少?(用含m的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com