
【题目】为迎接2019年的到来,铜陵万达广场某商铺将进价为40元的礼盒按50元售出时,能卖出500盒.商铺发现这种礼盒每涨价0.1元时,其销量就减少1盒.
(1)若该商铺计划赚得9000元的利润,售价应定为多少元?
(2)物价部门规定:该礼盒售价不得超过进价的1.5倍.问:此时礼盒售价定为多少元,才能使得商铺的获利最大?且最大利润为多少元?
【答案】(1)售价应该定位70元;(2)售价为60元时,最大利润为800元.
【解析】
(1)设涨价为x元,那么就少卖出![]() 个,根据单价为40元的商品按50元售出时,能卖出500盒,已知这种商品每涨价0.1元时,其销量就减少1盒,为了赚得9000元的利润,可列方程求解.
个,根据单价为40元的商品按50元售出时,能卖出500盒,已知这种商品每涨价0.1元时,其销量就减少1盒,为了赚得9000元的利润,可列方程求解.
(2)列出有关利润与涨价的函数关系式求得最值即可.
(1)设涨价为x元,根据题意得:
(50+x﹣40)(500﹣![]() )=9000,
)=9000,
(x﹣20)2=0,
x1=x2=20,
所以定价为:20+50=70元,
所以售价应该定位70元,该商铺可赚得9000元的利润;
(2)设该商铺的利润为y元,根据题意得:
y=(50+x﹣40)(500﹣![]() )=﹣10(x﹣20)2+9000,
)=﹣10(x﹣20)2+9000,
∵该礼盒售价不得超过进价的1.5倍,
∴50+x≤1.5×40,
∴x≤10,
∴当x=10时有最大利润﹣10(10﹣20)2+9000=8000,
此时售价为50+10=60元,
∴当售价为60元时,最大利润为800元.


科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=10,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
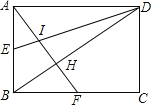
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x+8的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.

(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOB,求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )
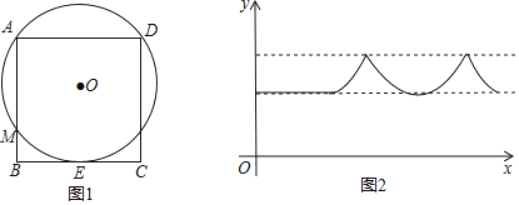
A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在湖北武汉举行,这是中国首次承办世界军人运动会.现有两张纪念卡片分别绘有会徽和吉祥物的图案(如下图),纪念卡背面完全相同.

(1)小丽从两张纪念卡任意摸一张,则小丽摸到绘有吉祥物“兵兵”的概率为______;
(2)如果小丽摸两次(第一次摸出后记录并放回),求小丽两次摸到的纪念卡相同的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC 中,AB=AC.
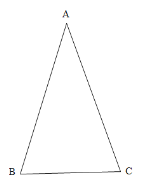
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC.
(操作)(1)将△ABD绕点D沿顺时针方向旋转60°,在图中画出旋转后的三角形.
(探究)(2)结合所画图形探究BD与AB,BC之间的数量关系,并证明你的结论.
(应用)(3)若AB=6,BC=8,试求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com