
【题目】如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_____度.

【答案】45
【解析】分析:首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后可求出∠AFD,∠CFE的度数.
详解:连接AC,
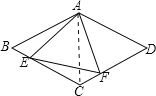
∵菱形ABCD,∴AB=BC,∠B=∠D=60°,
∴△ABC为等边三角形,∠BCD=120°
∴AB=AC,∠ACF=![]() ∠BCD=60°,
∠BCD=60°,
∴∠B=∠ACF,
∵△ABC为等边三角形,
∴∠BAC=60°,即∠BAE+∠EAC=60°,
又∠EAF=60°,即∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE与△ACF中
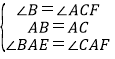
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AFD=180°-45°-60°=75°,
则∠CFE=180°-75°-60°=45°.
故答案为:45.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;②m是方程m2 -12=0的解;③m满足不等式组![]() ,④m是12的算术平方根.
,④m是12的算术平方根.
A. ①② B. ①③ C. ③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
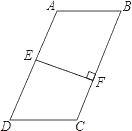
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图像交
的图像交 ![]() 轴于
轴于 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() ,连接直线
,连接直线 ![]() .
.
(1)求二次函数的解析式;
(2)点 ![]() 在二次函数的图像上,圆
在二次函数的图像上,圆 ![]() 与直线
与直线 ![]() 相切,切点为
相切,切点为 ![]() .
.
①若 ![]() 在
在 ![]() 轴的左侧,且△
轴的左侧,且△ ![]() ∽△
∽△ ![]() ,求点
,求点 ![]() 的坐标;
的坐标;
②若圆 ![]() 的半径为4,求点
的半径为4,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:

(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由;
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论;
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC,点M是平面上一点,射线BM与直线AC交于点D,射线CM与直线AB交于点E.过点A作AF∥CE,AF与BC所在的直线交于点F.

(1)如图1,当BD⊥AC,CE⊥AB时,写出∠BAD的一个余角,并证明∠ABD=∠CAF;
(2)若∠BAC=80°,∠BMC=120°.
①如图2,当点M在△ABC内部时,用等式表示∠ABD与∠CAF之间的数量关系,并加以证明;
②如图3,当点M在△ABC外部时,依题意补全图形,并直接写出用等式表示的∠ABD与∠CAF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年端午节前夕,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
商品 单价(元/件) | 成本价 | 销售价 |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com