Question

已知抛物线y=-x²+2（m-3）x+m-1与x轴交于B，A两点，其中B在x轴的负半轴上，点A在x轴的正半轴上，该抛物线与y轴交于点C．
（1）写出抛物线的开口方向与点C的坐标（用含m的式子表示）；
（2）若tan∠CBA=3，试求抛物线的解析式；
（3）设点P（x，y）（其中0＜x＜3）是（2）中抛物线上的一个动点，试求四边形AOCP的面积的最大值及此时点P的坐标．

Answer 1

分析：（1）二次函数的二次项系数是-1＜0，因而抛物线的开口向下．在函数解析式中令x=0解得y的值，就是C的纵坐标；
（2）解方程-x²+2（m-3）x+m-1=0得到方程的两个根，tan∠CBA=3，就可以转化为OB，OC之间的关系，就可以用m表示出B点的坐标，把B点的坐标代入抛物线的解析式，就可以得到一个关于m的方程，从而解出m的值．得到函数的解析式；
（3）四边形AOCP的面积为S_△COP+S_△OPA，这两个三角形的面积就可以用x表示出来，从而把面积表示成x的函数，转化为函数的最值问题．

解答：解：（1）抛物线的开口向下，点C的坐标是（0，m-1）；

（2）∵点A、B分别在x轴的正、负半轴上，
∴方程-x²+2（m-3）x+m-1=0的两根异号，
即m-1＞0，
∴OC=m-1，由tan∠CBA=3，
得OB=

1

3

OC=

1

3

（m-1），
∴点B的坐标为（-

m-1

3

，0），
代入解析式得-

1

9

（m-1）²-

2

3

（m-1）（m-3）+m-1=0，
由m-1≠0得-

1

9

（m-1）-

2

3

（m-3）+1=0，
∴m=4，
抛物线的解析式为y=-x²+2x+3；

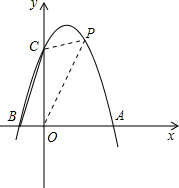
（3）如图，当0＜x＜3时，y＞0，
∴四边形AOCP的面积为S_△COP+S_△OPA=

1

2

×3x+

1

2

×3y
=

3

2

（x-x²+2x+3）=-

3

2

（x-

3

2

）²+

63

8

∴当点P的坐标为（

3

2

，

15

4

）时，四边形AOCP的面积达到最大值

63

8

，
说明：①四边形AOCP有多种分割方法，殊途同归，都可得S=

3

2

（x+y）．
②点P坐标忘了求，其余正确的给（13分）．

点评：本题是三角函数与二次函数几何图形相结合的综合题，难度较大．