
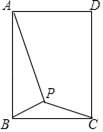
【题目】如图,在矩形ABCD中,AB=8,BC=5,P是矩形内部一动点,且满足∠PAB=∠PBC,则线段CP的最小值是_______.
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )
A. AB=c,AC=b,BC=a,DE=![]() ,EF=
,EF=![]() ,DF=
,DF=![]()
B. AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1
C. AB=3,AC=4,BC=6,DE=12,EF=8,DF=6
D. AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,DE=
,DE=![]() ,EF=3,DF=3
,EF=3,DF=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道.

(1)现有一辆卡车装满家具后,高为3.6米,宽为3.2米,请问这辆送家具的卡车能通过这个通道吗?为什么?
(2)如图2,若通道正中间有一个0.4米宽的隔离带,问一辆宽1.5米高3.8米的车能通过这个通道吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
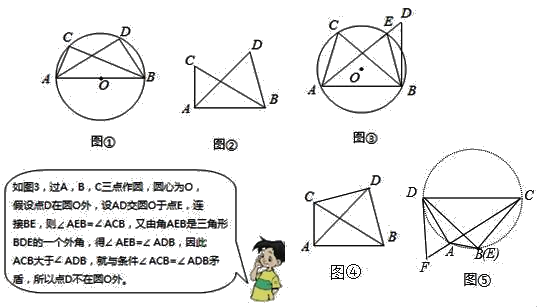
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 同时满足下列条件:①对称轴是
同时满足下列条件:①对称轴是![]() ;②最值是
;②最值是![]() ;③图象与
;③图象与![]() 轴有两个交点,其横坐标的平方和为
轴有两个交点,其横坐标的平方和为![]() ,则
,则![]() 的值是( )
的值是( )
A. 4或-30 B. -30 C. 4 D. 6或-20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com