
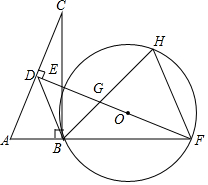
 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.分析 (1)根据ASA或AAS即可证明;
(2)结论:BD与⊙O相切. 连接OB,只要证明OB⊥BD即可;
(3)连接EH,首先证明△GHF∽△FHB,可得$\frac{HF}{HB}$=$\frac{HG}{HF}$,即HG•HB=HF2,想办法求出HF2即可解决问题.
解答 (1)∵DF⊥AC,△ABC为Rt△,
∴∠CDE=∠EBF=90°
∵∠CED=∠FEB,
∴∠DCE=∠EFB,
在△ABC和△EBF中,
$\left\{\begin{array}{l}{∠ACB=∠EFB}\\{BC=BF}\\{∠ABC=∠EBF=90°}\end{array}\right.$,
∴△ABC≌△EBF,(ASA).
(2)结论:BD与⊙O相切.
理由:连接OB,
∵DF是AB的中垂线,∠ABC=90°,
∴DB=DC=DA,
∴∠DBC=∠C.
由(1)∠DCB=∠EFB,而∠EFB=∠OBF,
∴∠DBC=∠OBF,
∴∠DBO=∠DBC+∠EBO=∠OBF+∠EBO=90°,
∴DB⊥OB,
∴BD与⊙O相切.
(3)连接EH,
∵BH是∠EBF的平分线,
∴∠EBH=∠HBF=45°.∠HFE=∠HBE=45°.
又∠GHF=∠FHB,
∴△GHF∽△FHB,
∴$\frac{HF}{HB}$=$\frac{HG}{HF}$,
∴HG•HB=HF2,
∵⊙O是Rt△BEF的内接圆,
∴EF为⊙O的直径,
∴∠EHF=90°,
又∠HFE=45°,
∴EH=HF,
∴EF2=EH2+HF2=2HF2,
在Rt△ABC中,AB=1,tan∠C=$\frac{1}{2}$,
∴BC=2,AC=$\sqrt{A{B^2}+BC{\;}^2}=\sqrt{{1^2}+{2^2}}=\sqrt{5}$,
由(1)知△ABC≌△EBF,
∴EF=AC=$\sqrt{5}$,
∴2HF2=EF2=5,
∴HF2=$\frac{5}{2}$,
故HG•HB=HF2=$\frac{5}{2}$.
点评 本题考查圆综合题、切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,正确相似三角形解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
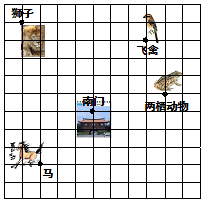 这是一个动物园游览示意图,如果以南门为坐标原点,东西为x轴,南北为y轴,
这是一个动物园游览示意图,如果以南门为坐标原点,东西为x轴,南北为y轴,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
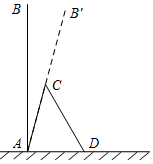 一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com