
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
分析 (1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;
(2)根据两个取值先计算:当1≤x<9时和9≤x<15时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比;
(3)设第15天在第14天的价格基础上最多可降a元,根据第15天的利润比(2)中最大利润最多少127.5元,列不等式可得结论.
解答 解:(1)设该种水果每次降价的百分率是x,
10(1-x)2=8.1,
x=10%或x=190%(舍去),
答:该种水果每次降价的百分率是10%;
(2)当1≤x<9时,第1次降价后的价格:10×(1-10%)=9,
∴y=(9-4.1)(80-3x)-(40+3x)=-17.7x+352,
∵-17.7<0,
∴y随x的增大而减小,
∴当x=1时,y有最大值,
y大=-17.7×1+352=334.3(元),
当9≤x<15时,第2次降价后的价格:8.1元,
∴y=(8.1-4.1)(120-x)-(3x2-64x+400)=-3x2+60x+80=-3(x-10)2+380,
∵-3<0,
∴当9≤x≤10时,y随x的增大而增大,
当10<x<15时,y随x的增大而减小,
∴当x=10时,y有最大值,
y大=380(元),
综上所述,y与x(1≤x<15)之间的函数关系式为:y=$\left\{\begin{array}{l}{-17.7x+352(1≤x<9)}\\{-3{x}^{2}+60x+80(9≤x<15)}\end{array}\right.$,
第10天时销售利润最大;
(3)设第15天在第14天的价格基础上最多可降a元,
由题意得:380-127.5≤(4-a)(120-15)-(3×152-64×15+400),
252.5≤105(4-a)-115,
a≤0.5,
答:第15天在第14天的价格基础上最多可降0.5元.
点评 本题考查了一元二次方程的应用及二次函数的有关知识,解题的关键是正确的找到题目中的等量关系且利用其列出方程,注意第2问中x的取值,两个取值中的最大值才是最大利润.


科目:初中数学 来源: 题型:解答题
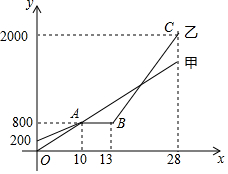 甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.
甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
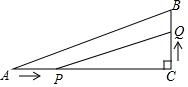 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )| A. | 20cm | B. | 18cm | C. | 2$\sqrt{5}$cm | D. | 3$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
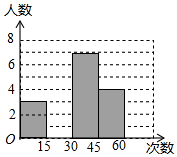 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | a | 0.3 |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | 4 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
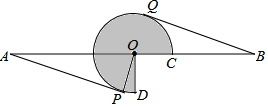 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.
如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高/cm | 159 | 160 | 161 | 162 |
| 人数 | 7 | 10 | 9 | 9 |
| A. | 160和160 | B. | 160和160.5 | C. | 160和161 | D. | 161和161 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
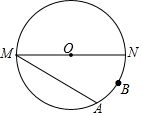 如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.
如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
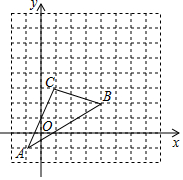 △ABC在直角坐标系中位置如图所示,把△ABC向右平移3个单位,再向上平移1个单位得△A′B′C′.
△ABC在直角坐标系中位置如图所示,把△ABC向右平移3个单位,再向上平移1个单位得△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com