
����Ŀ���Ķ����⣺��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ���2�������ǾͳƵ�C�ǣ�A��B�����õ���
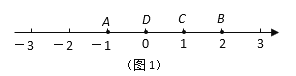
���磬��ͼ1����A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǣ�A��B���ĺõ㣻
���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D��������A��B���ĺõ㣬����D�ǣ�B��A���ĺõ㣮
֪ʶ���ã���ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4.
��1����_______________________ ����ʾ�ĵ��ǣ�M��N���ĺõ㣻
��2����________________________ ����ʾ�ĵ��ǣ�N��M���ĺõ㣻

����ܰ��ʾ��ע�⿼��M��N����ࡢ�Ҳ࣬��Ҫ©���𰸣�
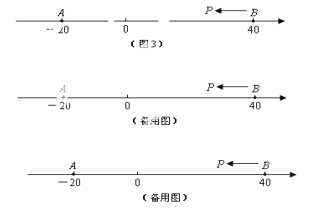
��3����ͼ��3��A,BΪ�����ϵ����㣬��A����ʾ����Ϊ-20����B��ʾ����Ϊ 40������һֻ��������P�ӵ�B��������2��λÿ����ٶ�һֱ�����˶���
�ٵ�tΪ��ֵʱ��P�ǣ�A��B���ĺõ㣿
�ڵ�tΪ��ֵʱ��P�ǣ�B��A���ĺõ㣿
���𰸡���1��2��10����2��0��-8����3����t=10����t=20��60
��������
��1����������Ϊx�����ݺõ�Ķ����г����̣��ⷽ�̼��ɣ�
��2����������Ϊy�����ݺõ�Ķ����г����̣��ⷽ�̼��ɣ�
��3���ٸ��ݺõ�Ķ����г����̣��ⷽ�̼��ɣ�
�ڸ��ݺõ�Ķ����г����̣��ⷽ�̼��ɣ�
�⣺��1����������Ϊx���������
x-��-2��=2��4-x������x-��-2��=2��x-4����
���x=2��10��
�ʴ�Ϊ��2��10��
��2��2[y-��-2��]=4-y��2��-2-y��=4-y
���x=0��-8��
�ʴ�Ϊ��0��-8��
��3����PΪ��A��B���ĺõ㣮
�����⣬��60-2t=4t��
���t=10��
��PΪ��B��A���ĺõ㣮
�������2��60-2t��=2t����2t=2��2t-60��
���t=20��60


 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ضԽ���BD�۵�����C���ڵ�E����BE��AD�ڵ�F����֪��BDC=62��������EDF�Ķ���Ϊ�� ��

A.34��B.56��C.62��D.28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
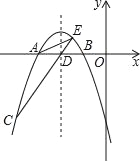
����Ŀ����ͼ��������y=��![]() x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
��1���������ߵĽ���ʽ��
��2���������ߵĶ������꼰��B�����ꣻ
��3���������ߵĶԳ�����x�ύ�ڵ�D������CD�����ӳ�CD���������ڵ�E������AC��AE������ACE�������
��4������������һ������M����A��B���㹹����ABM���Ƿ����S��ADM=![]() S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�������ɸ�СԲȦ�ѳɵ�һ������ȱ������ε�ͼ����������һ����һ��ԲȦ��
���¸��������һ���һ��ԲȦ��һ������n �㣮��ͼ1���ú���ԭͼ1ƴ��ͼ2����״���������ǿ���
���ͼ1������ԲȦ�ĸ���Ϊ1��2��3������n��![]() ��
��

���ͼ�е�ԲȦ����13�㣬�����������⣺
��1�������������£���ÿ��ԲȦ�а�ͼ3�ķ�ʽ����һ��������������1��2��3��4������������ײ�����
�����ԲȦ�е����� ��
��2�������������£���ÿ��ԲȦ�а�ͼ4�ķ�ʽ����һ��������������23����22����21����20����������
��ײ����ұ�ԲȦ�ڵ�����_______��
��3����ͼ4������ԲȦ�и����ľ���ֵ֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
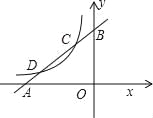
����Ŀ����ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ��ڵ�A��B����˫����![]() ��x��0���ֱ��ڵ�C��D����C�������Ϊ����1��2����
��x��0���ֱ��ڵ�C��D����C�������Ϊ����1��2����
��1���ֱ����ֱ��AB��˫���ߵĽ���ʽ��
��2�������D�����ꣻ
��3������ͼ��ֱ��д������x��ʲô��Χ��ȡֵʱ��y1��y2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������Ƥ�����ĸ��Ǹ���ȥһ���߳�Ϊ2�������κ�ʣ�µIJ�������һ���ݻ�Ϊ90�������dz��������ӣ���֪���������ӵ���ij��ȿ���4�ף��������Ƥ�������
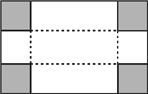
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD��80cm��AB��40cm���뾶Ϊ8cm�ġ�O�ھ���������AB��AD�����У����ж���P��A��������ھ��α�������A��B��C��D�ķ��������ƶ�������P����D��ʱֹͣ�ƶ�����O�ھ����ڲ���AD��������ƽ�ƣ��ƶ�����CD����ʱ������ԭ·��ԭ�ٷ��أ�����O�ص�����ʱ��λ�ã����ٴ���AB���У�ʱֹͣ�ƶ�����֪��P���Oͬʱ��ʼ�ƶ���ͬʱֹͣ�ƶ�����ͬʱ������Ե���ֹλ�ã�������O�����O1��λ��ʱ����ʱԲ��O1�ھ��ζԽ���BD�ϣ���DP���O1ǡ�����У���ʱ��O�ƶ��ˣ�������cm��
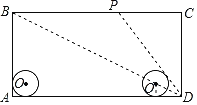
A.56B.72C.56��72D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E�Խ���BD�ϣ��ҡ�BAE=22.5����EF��AB������Ϊ��F����EF�ij�Ϊ�� ��
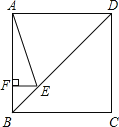
A. 1B. 4-![]() C.
C. ![]() D.
D. ![]() -4
-4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������Ҫ�øֹ����������������Ҫ��������Ҫ��Ϊ 0.8m��2.5m �Ҵ�ϸ��ͬ�ĸֱֹܷ�Ϊ 100 ����32 ������Ҫ����Щ���ϲ����Ǻ��Ӷ��ɵģ��ֲָ��г������ֹ��ĸֹ�ÿ��Ϊ 6m��
��1������һ�� 6m ����Բ�ֹ�����Щ�ü������أ�����д�¿գ��������ϣ���
�����٣���ֻ�ü���Ϊ 0.8m ������ʱ�����ɼ� ����
�����ڣ����ȼ��� 1 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
�����ۣ����ȼ��� 2 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
��2���ֱ��ã�1���еķ����ںͷ����۸��ü����ٸ� 6m ���ĸֹܣ����ܸպõõ�����Ҫ����Ӧ�����IJ��ϣ�
��3����̽��������2���з����⣬�ڣ�1���л��������ַ������ϣ�����Ҫ 6m ���ĸֹ��루2�� �и�����ͬ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com